Sur les traces de Lévi-Strauss, Lacan et Foucault, filant comme le sable au vent marin...
20 Juin 2020
- Je te propose de partir de nos dernières réflexions suscitées par une discussion née d'un rapprochement entre le langage catégorique et les figures de styles que sont la métonymie et la métaphore, récupérées par les psychanalystes (voir ici). Reporte-toi au passage suivant de ma dernière note:
Lorsque je parle d'orthogonalité entre concepts, il faut entendre ceci : la répétition du saut I01↑IR permet d'ajouter à chaque fois une dimension orthogonale aux précédentes, ce qui nous ramène à mes développements autour du concept d'homologie (voir "Les groupes d'homologie du Sujet").
Pour faire simple :
Autrement dit, à chaque itération du saut I01↑IR, j'ajoute une dimension "orthogonale" au concept synchronique déjà identifié à l'étape précédente.
Mais, et c'est là qu'il faut faire attention, pour "repérer" un objet dans son environnement, il faut adopter une approche topologique consistant à le plonger dans un espace d'ordre supérieur :
D'où l'importance, en passant, des quaternions de Hamilton en physique (voir "Hamilton, réalité du temps et espace imaginaire").
- Est-ce à dire qu'au fur et à mesure que le Sujet complexifie son Imaginaire, le principe diachronique de l'étape précédente, marque sa différence par rapport à ce qui est déjà réifié par son orthogonalité ?
- Exactement. D'où l'intérêt d'une représentation en volume des rapports entre morphismes/ foncteurs/ transformations naturelles.
- Ça pose un problème de taille, car le contexte pour parler de 3D, c'est un cadre en 4D ! le tableau noir de notre enfance se transforme en vidéo.
- Certes, mais en procédant ainsi, tout devient simple, voire trivial !
- Tu as pu voir que pour réfuter un raisonnement basé sur l'opposition contenant/ contenu, concepts en 3D, le plus simple est encore de les plonger dans un espace en 4D pour poser la question qui tue: où est l'intérieur, où est l'extérieur ?"
J'étais assez satisfait de cette mise au point, qui me permettait de trouver une façon élégante, me semblait-il, de réfuter mon contradicteur.
- Qu'est-ce que l'élégance vient faire là-dedans ?
- Elle a tout à y voir. À mes yeux, un objet, qu'il soit matériel ou une simple construction intellectuelle, est élégant lorsqu'il est simple, voire minimaliste. Or, c'est bien ce que nous recherchons ici, n'est-ce pas ?
- À savoir ?
- Représenter de la façon la plus simple possible, la posture du Sujet lorsqu'il prend conscience du Monde qui l'entoure et l'exprime dans son discours.
- Il s'agit au sens propre d'une réflexion du Sujet sur lui-même !
- Oui, et c'est toute la difficulté de la chose, du même ordre que le paradoxe de Russell en théorie des Ensembles:
"l'ensemble des ensembles n'appartenant pas à eux-mêmes appartient-il à lui-même?"
Ici se pose la question de ma propre posture lorsque je prétends exprimer celle d'un Sujet : ce dernier est irrémédiablement l'Autre de ma propre personne, et donc ce que j'en dis me reste étranger. Ça renvoie également à Gödel :
"Si T est une théorie cohérente, la cohérence de T, n'est pas démontrable dans T."
- Merci pour la leçon, mais tu nous balades !
- Au contraire, je te mène au fond du problème en te montrant que l'on ne peut jamais figer l'objet de notre propos, car il s'échappe toujours d'une façon ou d'une autre.
- Et donc, on en revient à Wittgenstein et l'on se tait ?
- Non ! Si l'on ne peut pas le cerner complètement, on peut toutefois parler de l'expérience que l'on en a...
- D'où l'importance du langage catégorique ?
- Oui, c'est la voie qui me semble la plus indiquée pour un Occidental.
- Qu'est-ce que l'Occident vient faire dans l'histoire ?
- Parce que notre cheminement est historiquement balisé par Aristote, Galilée, Descartes, Galois, Noether, etc., comme autant de points d'appuis qui nous permettraient de traverser un ruisseau. Nous sommes au milieu du gué et devons choisir où poser le pied pour avancer d'un pas à partir de notre position actuelle.
Une pensée Orientale, qui se développerait à partir de Lao Tseu, du Yi King ou de Bouddha ne suivrait sans doute pas la même voie, parce qu'elle intègre déjà, primitivement, l'idée que tout part du mouvement et de la circulation d'une énergie. Mais ça ne nous empêche pas de lever le nez de notre propre voie pour voir ce qui se passe alentour, et constater que nous allons peu ou prou dans la même direction, le point à l'horizon de notre perspective.
- Belle envolée, mais concrètement ?
- Le point stable de notre civilisation c'est la pensée rationnelle logique, initiée ou formalisée par Descartes (voir "Le cogito Cartésien"). Le pas suivant, tout aussi important, a été initié par Évariste Galois. Il s'agit de l'approche topologique. Cependant, bien qu'elle inonde complètement les mathématiques modernes, bien peu de mathématiciens comprendraient que je fasse le distinguo entre ces deux postures, persuadés qu'ils sont d'être "Cartésiens" !
- Où est le problème ?
- Le mathématicien cherche à s'extraire au maximum de son discours. Il ne veut considérer que des "objets". Ça lui saute à la figure de toute part, voir Russell et Gödel, mais il s'accroche !
- Il doit pourtant s'accrocher à quelques axiomes qui échappent à la démonstration mathématique, non ?
- Bien sûr, mais il le vit très mal ! Ce sont des croûtes purulentes qui s'infectent d'autant plus qu'il les gratte...
- D'accord, d'accord, mais avance un peu, tu feras ton discours une autre fois, quel rapport avec cette note de fond d'article ?
- Eh bien, précisément, j'y parle du mouvement du Sujet autour de l'objet.
C'est l'opposition dénoter/ connoter qui m'a rappelé Lévi-Strauss nous expliquant la différence entre pensée rationnelle (R<Im) et pensée mythique (Im<S). L'approche topologique apparaît alors comme un cadrage rationnel a priori d'une quête limitée aux potentialités définies par Im : I'm<I01<IR<Im.
- Mais tu nous a déjà dit tout ceci jusqu'à plus soif !
- Sans doute, mais ce n'est pas encore audible, semble-t-il.
- Parce que c'est trop compliqué.
- Ah ! Nous en revenons à l'élégance du propos. Eh bien figure-toi que j'ai trouvé un maître à qui me référer, pour t'inviter à faire l'effort de me comprendre: Grotendieck et son topos, qu'il voit comme le "nid commun du discret et du continu".
- Tu me renvoies à un objet ?
- Contresens, mon ami ! Le topos de Grothendieck n'est pas un objet mais un mouvement vers un lieu où se conjoignent le discret et le continu".
Présentation de Laurent Lafforgue
Reporte-toi en particulier à 15' de la vidéo.
- Tu ne vas pas nous faire un cours ?
- Non, pas ici, mais il est temps pour moi de situer ce topos dans ma propre approche, à partir de ce que nous avons déjà vu des morphismes, foncteurs et transformations naturelles.
La définition formelle qu'en donne ici Laurent Lafforgue est la suivante (voir à 18'):
"Un topos est une catégorie de faisceaux sur un site (C,J), où C est une catégorie et J une topologie de Grotendieck (c.-à-d. "une notion très générale de recouvrements" ).
Ça paraît un peu abscons lorsque tu abordes ça tout à trac, d'autant plus que Lafforgue lui-même présente (à 17'50") une catégorie comme un "objet combinatoire" composé d'objets et de flèches ! Ce qui prouve qu'il n'a pas fini de faire sa propre révolution intellectuelle car il n'a aucune conscience de la différence, essentielle à mes yeux, entre synchronie/ diachronie !
Pour mémoire, un morphisme est originellement un mouvement qui rapporte un élément d'un domaine vers un autre objet du codomaine, à tel point que l'on peut s'affranchir de la notion d'objet pour voir ce dernier comme un "mouvement se bouclant sur lui-même".
- Un peu comme de boucler la sortie d'un ampli op sur son entrée pour faire un "bit" élémentaire ?
- Oui, je vois que tu n'as pas perdu les notions d'automatisme de ta jeunesse !
Donc, le morphisme le plus primitif, c'est le morphisme identité de l'objet final sur le singleton: Id: (*)∈I1↑{1}∈I01, avec notre Sujet ex post, dans la posture rationnelle logique : I1<I01<Im. Lafforgue, lui, a déjà réifié (i.e.: aplati) ce mouvement par sa représentation sous forme de graphe (*)→{1} en I01<Im.
Venons-en à la catégorie des faisceaux: c'est essentiellement un foncteur contravariant d'une catégorie D dans une autre C; qui s'écrit F: Dop→C. Pour nous, si nous en revenons au fondement des revêtements, (voir "Identité et idempotence"), c'est une application d'un ensemble de morphismes ↓ plongeants (i.e: Dop), vu localement de I'm<, vers un ensemble de morphismes ↑ dans C, vu de <Im. Comme tu le vois, il y a une torsion dans cette représentation, qui est au coeur même de ce que j'ai définis comme une "approche topologique" !
- Comment se situent D et C dans ton feuilletage Imaginaire I1<I01<IR<I# ?
- C'est précisément ce qu'il est délicat de représenter simplement sur un tableau noir. Ils peuvent être tous deux de niveau IR, mais le plus intéressant, c'est le cas où tu rapportes une catégorie supérieure, (mettons D∈IR), à un niveau plus élémentaire, typiquement, la catégorie des Ensembles (i.e.: C∈I01). Dans ce dernier cas, ton foncteur contravariant apparaît comme un artifice permettant à <Im de se représenter un mouvement descendant vers I'm<, dans la situation très générale : I'm<I01<IR<Im.
Vois-tu toute la difficulté qu'il y a à exprimer ce mouvement de pensée?
Je te propose de le voir comme un "Foncteur plongeant" F↓, en gardant à l'esprit la dualité des point de vue : F↓ représente (note du 01/07/2020)
L'image que nous en avons, c'est donc une généralisation de ce qui serait un vecteur rapporté à une base. Cette "base" étant ici le site (C,J) de notre topos.
Maintenant, et c'est là qu'il te faut être attentif, ce site est explicitement le lieu où tu peux décrire un "objet" selon nos deux points de vue :
Ce qui compte avant tout, c'est le mouvement du Sujet autour de C.
Pour te fixer les idées, limite ta réflexion à l'objet final (*).
- Sauf que là, ta topologie est bien maigre, sans continuité ni ouvert etc...
- Oui, on parle ici de "pré-faisceaux", en considérant la catégorie la plus simple, celle des Ensembles. Mais il était important de faire régresser les concepts jusqu'à cette limite pour faire le lien entre le topos de Lawvere (avec l'objet discriminant) et celui de Grothendieck (muni d'une topologie comprenant la notion d'ouvert), grâce à cette communauté des postures du Sujet.
Et pour le dire tout d'un trait :
À tel point, et c'est là où je voulais nous mener, que je me demande si l'on ne pourrait pas, tout simplement caractériser pleinement ces deux niveaux Imaginaires de cette façon, en inversant les propositions:
- Soit, mais quid des topoï eux-mêmes ?
- Tu as raison, nous n'avons fait que la moitié du chemin :
Ouf, je crois que ça s'éclaire, non ?
- Ça s'éclaire, ça s'éclaire... C'est très relatif, ça me semble bien compliqué malgré tout, pour quelqu'un qui veut rendre les choses simples et élégantes...
- Parce que tu regardes mal les choses. Voit ceci comme un couple Objet/ Sujet valsant, l'un autour de l'autre. Ce qui marque la place de l'Objet, c'est le mouvement du Sujet autour de lui, ce qui permet réciproquement au Sujet de se repérer.
Nous avons bel et bien le mouvement à la source de notre expérience du monde, et nos "objets" sont simplement ce que nous reconstruisons comme constant dans notre cerveau pour s'extraire d'une gesticulation sans fin et exister...
- Je reste malgré tout sur ma faim. Je m'attendais à ce que tu tire un lapin du chapeau.
- D'accord. Reprends le raisonnement de notre ami.
Il était faux, tout simplement parce qu'il pensait que les foncteurs manipulaient des "objets", alors qu'il s'agit d'une application entre catégories (i.e.: autrement dit d'objets ET d'applications). Mais cette réfutation est d'ordre dialectique, assez triviale au demeurant: "tu as tort et j'ai raison", point barre.
Mais son approche exprimait une préoccupation plus profonde, avec l'idée que certains "objets" sont des "contenants", et certains autres des "contenus". J'ai pris l'exemple de la déformation d'un tessarac pour réfuter cette opposition. Ce qui me demandait de me situer dans un espace en 4D pour réfuter un concept en 3D. Mais en y repensant, je me suis dit que c'était utiliser un marteau-pilon pour casser une noix: il suffisait de parler de topologie. Chacun sait qu'en topologie il n'y a aucune différence entre une balle et un bol, et qu'il est possible de passer continûment de l'un à l'autre.
Puis, en méditant sur cette réflexion, je me suis rappelé qu'une "transformation continue" nécessite malgré tout de s'effectuer dans le temps, et me revoici avec 4 dimensions... Comme si l'esprit se resserrait autour de représentations physiques en 4D. Nous en avons déjà parlé ces derniers temps (voir "Psy-chic/ phys-hic").
- Je ne vois pas le rapport ?
- Lorsque l'on suit les matheux dans leurs développements, ils partent vite en vrille, avec des développements à l'infini et des objets plus gros que l'Univers, et le topos est l'outil qui va permettre à l'esprit de se débrider complètement.
Cependant, pour exprimer une expérience physique, ou tout simplement une impression visuelle, je pense (et ça c'est personnel) que nous ne sommes pas équipés pour comprendre sensiblement au-delà de 4D. Nos yeux reconstituent un tableau en 3D, notre mémoire pédale pour reconstituer le temps, mais au-delà de 4D, ça reste un exercice de pur langage. C'est le rôle du niveau suivant I# de nous rappelez la relativité de toute chose.
Eh bien, je pense que pour aller au-delà de la dialectique traditionnelle, celle qui nous sert à argumenter, ou réfuter une proposition, il faut sauter à 4D. Le mouvement est en 4D.
Ce qui questionne en termes philosophiques les échecs répétés de Hamilton à concevoir un objet en 3D comparable au nombre complexe en 2D (l'ensemble C). Il n'a pas pu y arriver, mais il a découvert le Hamiltonien, en 4D (l'ensemble H).
Très concrètement, il me semble nécessaire de nous habituer à articuler notre pensée en 4D en nous entraînant à manier les topos, ce qui serait une "hyper-dialectique".
- Toi, tu penses à la psycho-histoire de Seldon !
- Laisse-moi rêver !
Imagine les Orateurs de la seconde Fondation sur Trantor, assemblés autour de la table du conseil de l'Université. Quelqu'un se lève et commence un développement s'appuyant sur la différence contenant/ contenu. Le Premier Orateur émet alors un léger raclement de gorge accompagné d'un "en 3D ?" à peine susurré, et la salle bruisse alors d'une rumeur légèrement ironique...
Elle serait dans cet instant de compréhension, l'élégance dont je parle ici ! ;-)
Hari
Note du 21/06/2020 :
Comme par hasard, les statistiques d'aujourd'hui m'indiquent qu'un article oublié est passablement lu ces temps-ci, que j'avais intitulé initialement (c'est le nom du lien): "mouvement et réflexion" :
Tu verras qu'en fait mes idées n'ont pas tellement évoluées depuis 2014 ... Alors que j'étais à cent lieux d'imaginer m'intéresser un jour à la théorie des catégories !
Note du 29/06/2020 :
Ce matin je m'aperçois que mon article
est encore lu, ce qui me tire l'oeil et par curiosité, je le relis, pour me faire la réflexion que mes lecteurs ont plus de mémoire que moi !
Il s'avère en effet qu'à cette époque, je traitais déjà du topos de Lawvere, que je situais en I01, dans le même esprit qu'ici.
J'ai corrigé ce passage hier, pour arriver à un résultat qui me satisfaisait sur le coup, et au fil de l'après-midi, une petite voix de plus en plus insistante s'est frayé un chemin jusqu'à ma conscience :
- Mais comment fais-tu le lien entre cette présentation d'un foncteur contravariant et celle à laquelle tu t'étais arrêté dans ta présentation du 12 juin de l'année dernière? Pour mémoire :
Foncteurs covariants et contravariants
Maintenant, il faut distinguer entre deux façons symétriques de faire ce rattachement. Notre objet A étant un élément du domaine de F, alors :
F est dit covariant : lorsque A est le domaine commun de Â;
F est dit contravariant : A est le codomaine commun de Â.
| Â =Hom (- ;A) : X⟼Hom (X ; A) | Â =Hom (A; -) : X⟼Hom (A ; X) |
 |
 |
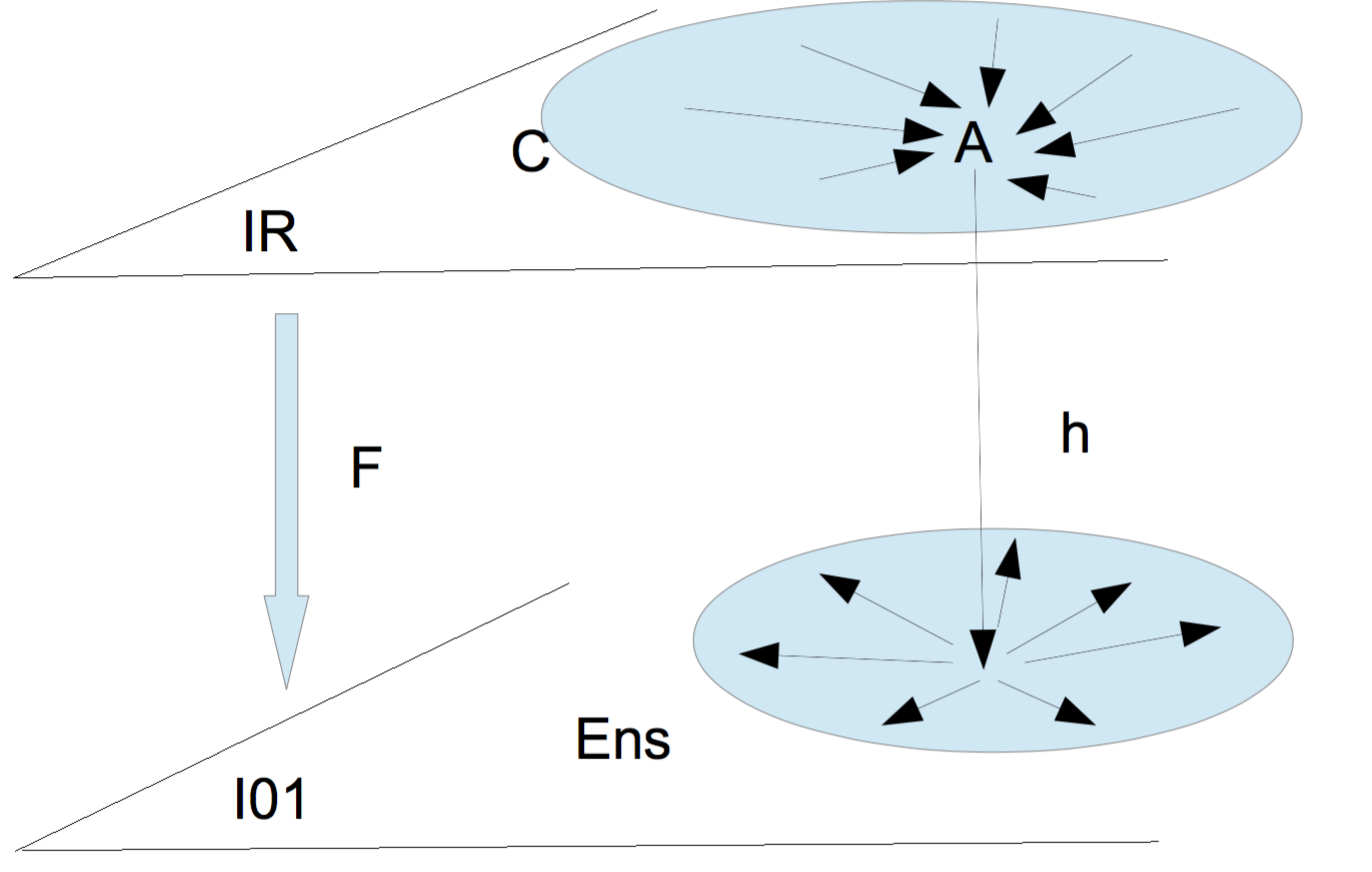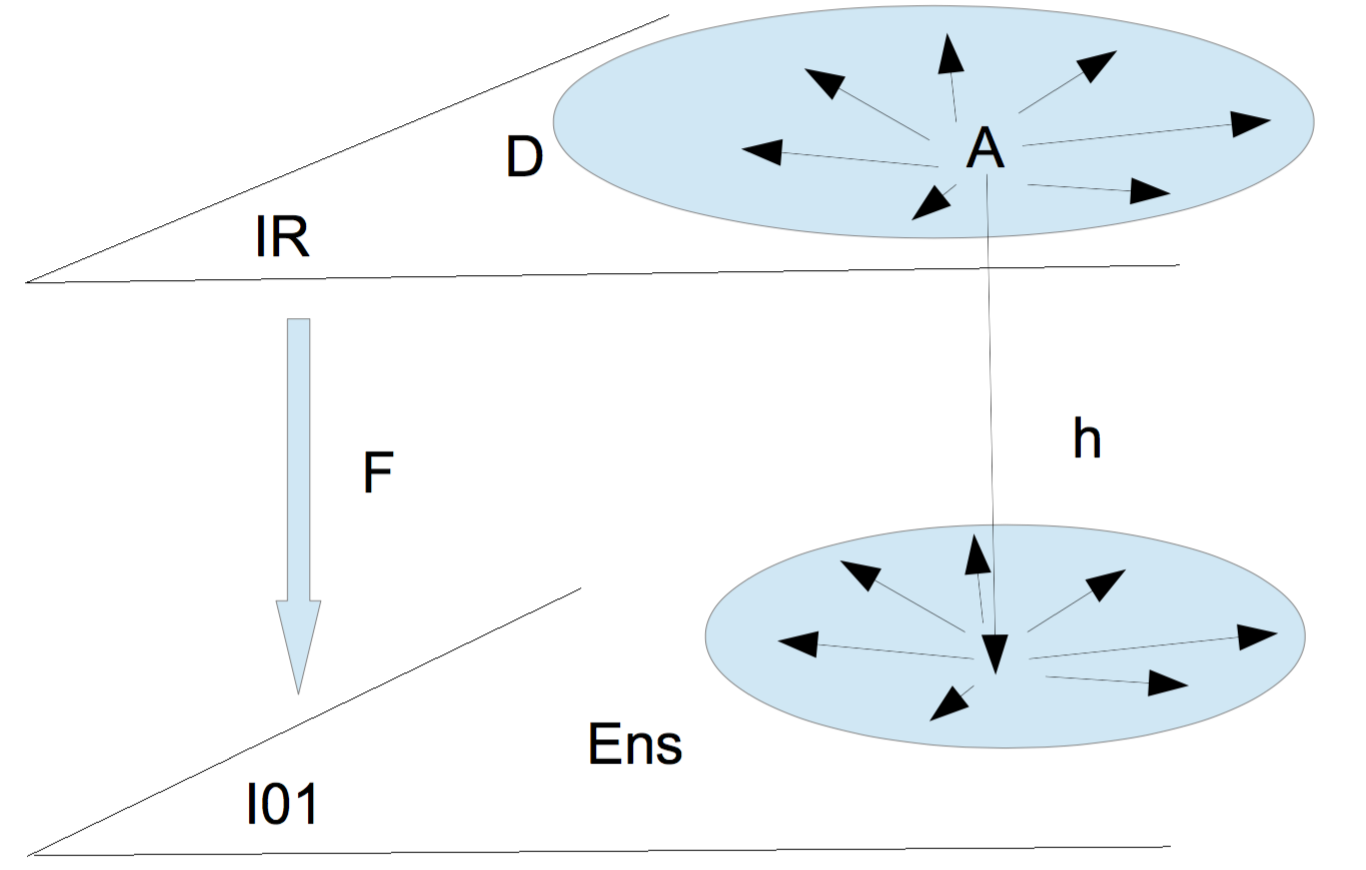| F contravariant | F covariant |
fig. 2
Tu noteras une différence fondamentale sur laquelle nous reviendrons (note du 08/03/2020):
- Tu as raison, je pense que ma propre pensée n'a pas encore parfaitement décanté ces concepts.
L'idée qui me vient, là pour l'instant, c'est que le point F(A)∈Ens peut être vu par Im, comme la projection en I01 de l'objet final (*) en I1, dans la position I1<I01<Im. L'équivalent pour la géométrie projective du point aveugle d'où partent toutes les droites projectives.
Si la posture du Sujet ne change pas lorsqu'il s'éloigne pour englober I01 et IR, le même schéma permet de voir A∈C comme "projection" de (*) en C, dans la position I1<I01<IR<Im. Et nous retrouvons notre fonceur "covariant", dans une posture qui ne cesse d'être "rationnelle logique".
- Et pour ton foncteur contravariant ?
- Il faut que C soit appréhendé localement en I'm<IR. En tournant le regard vers l'objet initial, on peut comprendre que A ne puisse être défini que par son entourage au sein de C. L'aspect "contravariant" tient alors, comme nous l'avons vu, au "changement de posture" du Sujet.
- Je veux bien, cependant, dans ton schéma, tes foncteurs, qu'ils soient covariants ou contrariants, sont descendant d'une catégorie quelconque vers Ens...
- Oui, sans doute, il faudrait parler de foncteurs conjoints...
Je me dis que la difficulté tient à ma propre position dans l'histoire.
La représentation développée dans cet article se focalise sur une rotation de I'm passant de I01<I'm à I'm<IR, tandis que dans mon article de référence, j'insiste plutôt sur l'orthogonalité entre concepts au-dessus de I01.
Et c'est sans doute ce changement de perspective qu'il me faudra expliciter...
Nota du 03/07/2020 :
Synchronicité ou pas, en relisant un texte de 11/2018, je m'aperçois que j'étais déjà dans ce type d'interrogation (voir la dernière note) :
/image%2F0964014%2F20230913%2Fob_60556e_contre-temps-dessin-de-yuval-robichek.jpeg)
/image%2F0964014%2F20190426%2Fob_e92c79_l-insoutenable-legerete-de-l-etre.jpg)
/image%2F0964014%2F20210516%2Fob_13a772_cartes.jpg)
/image%2F0964014%2F20201119%2Fob_cffbb9_moebius.png)