11 Janvier 2021
/image%2F0964014%2F20210111%2Fob_0f977b_le-chat.jpg)
- Dans l'article précédent, nous venons de voir, de façon très schématique, quelle posture devait adopter l'auteur 𓂀 pour parler de l'expérience du Sujet 𓁝I𓁜.
Mais avant même d'approfondir dans cette voie, il me semble nécessaire de réfléchir un peu à cet objet particulier qu'est le discours (...)𓂀 produit par l'auteur.
- Il me semblait que ton axiome de clôture montrait simplement que tout discours rationnel (...)⇆𓂀 était limité (ou clos) par l'auteur en posture [♲]⇆𓂀 ?
- Effectivement, mais je voudrais reprendre ici ma réflexion à partir de ce que nous avions établi dans "exercices" :
- N'avais-tu pas développé ce thème dans l'article suivant "Le Sujet - être de parole et au delà" ?
- Si, si, mais je voudrais m'assurer ici d'avoir fait le tour de la question, en réfléchissant à la nature de cet artefact qu'est le discours de l'auteur.
- Je ne comprends pas trop où tu veux en venir ?
- Moi non plus, je cherche.
Il y a tout d'abord ces "données immédiates" de la conscience liés à notre représentation instinctive du mouvement, de l'espace et du temps.
En prenant pour exemple l'approche locale topologique, nous en étions arrivé à cette conclusion que le passage de (𓁝⇅[#]𓁜⏩𓁝[#]⊥𓁜)⇅𓂀 (1) décrit une procédure (i.e;: une succession d'étapes dans le temps).
Toutefois pour "comprendre" ce dont je parle, il faut que je puisse envisager explicitement la posture finale du Sujet ([#]⊥𓁜)𓂀 ce qui n'est possible qu'en [#]⊥𓂀 où je suis incapable d'ordonner⚤ des séquences puisque mon discours n'est plus linéaire, mais s'étale, de façon picturale, en tableau.
- N'as-tu pas dit hier qu'il est possible d'encapsuler les discours, et donc qu'en écrivant (1), tu as implicitement (((𓁝⇅[#]𓁜⏩𓁝[#]⊥𓁜)⇅𓂀)⊥𓂀)⇆𓂀 (2) ?
- En empilant les parenthèses, (((...)⇅𓂀)⊥𓂀)⇆𓂀 je ne suis pas sûr d'échapper à cette notion primitive du temps, parce je figure encore une procédure. Reprenons tout depuis le discours initial (1) :
La succession se repère ici par les parenthèses : (...)⏩((...))⏩(((...))) malgré mon désir de m'élever au niveau [♲]⇆𓂀 de mon propre Imaginaire.
- C'est peut-être le moment de parler d'orthographe ! Est-ce qu'en passant de la phase 1 à la phase 2, tu as réellement adopté la position [#]⊥𓂀 ?
- Je crois que tu as raison. En phase 2, mon discours doit s'articuler autour des orthogonalités⊥. Je ne peux donc écrire que (𓁝⇅[#]𓁜⊥𓁝[#]⊥𓁜)⊥𓂀. De même à l'étape suivante ne puis-je qu'indiquer l'équivalence⇆ des deux positions (𓁝⇅[#]𓁜⇆𓁝[#]⊥𓁜)⇆𓂀.
Dans ce cas, mon étagement 1/2/3 précédant serait plutôt une indication de la profondeur de mon discours, dans une orientation du texte qui ne serait plus horizontale (i.e.: ☯[∃] [⚤] [#] [♲] [∅]☯) mais verticale.
| niveau de 𓂀 | les discours de 𓂀 sur 𓁝I𓁜 |
| ☯ | |
| [∅] | |
| [♲] | (𓁝⇅[#]𓁜⇆𓁝[#]⊥𓁜)⇆𓂀 |
| [#] | (𓁝⇅[#]𓁜⊥𓁝[#]⊥𓁜)⊥𓂀 |
| [⚤] | (𓁝⇅[#]𓁜⇅𓁝[#]⊥𓁜)⇅𓂀 |
| [∃] | |
| ☯ |
Cette façon d'écrire me fait prendre conscience de l'orthogonalité entre les Imaginaires du Sujet (i.e.: ce qu'en dit 𓂀 se déploie horizontalement) et de l'auteur, repéré ici verticalement. Autrement dit, je suis dans un discours de niveau [#]⊥𓂀 ?
- Mais ce n'est pas cohérent avec (𓁝⇅[#]𓁜⇆𓁝[#]⊥𓁜)⇆𓂀 !
- Effectivement, il reste encore une dissonance à lever; mais tout au moins pouvons-nous écrire sans ambiguïté :
| niveau de 𓂀 | les discours de 𓂀 sur 𓁝I𓁜 |
| [#] | (𓁝⇅[#]𓁜⊥𓁝[#]⊥𓁜)⊥𓂀 (2) |
| [⚤] | (𓁝⇅[#]𓁜⇅𓁝[#]⊥𓁜)⇅𓂀 (1) |
Dans cette représentation en 2D, il n'y a plus succession dans les discours, mais concomitance : 𓂀 exprime "à la fois" (1) et (2) dans un espace :
| ☯[∃] [⚤] [#] [♲] [∅]☯ | |
| [#] | (𓁝⇅[#]𓁜⊥𓁝[#]⊥𓁜)⊥𓂀 |
| [⚤] | (𓁝⇅[#]𓁜⇅𓁝[#]⊥𓁜)⇅𓂀 |
- D'accord: ton discours s'inscrit ainsi sur deux Imaginaires orthogonaux, celui du Sujet et le tien, en tant qu'auteur. Mais quid de la posture finale ⇆𓂀 ?
- On en revient à la notion extrêmement basique que 𓂀 est un "Sujet" 𓁝I𓁜; ou "Je est un Autre" pour reprendre Lacan. Nous sommes déjà arrivé à ce constat que le Sujet, comme l'auteur doivent être considérés en [♲]⇆𓂀 comme un volume♲au regard d'une enveloppe#. Or, l'enveloppe, nous l'avons : c'est l'ensemble des discours engendrés par nos deux Imaginaires orthogonaux.
- Tu voudrais plonger cette surface en 2D dans un espace en 3D ?
- Oui, et ça semble assez évident, avec un peu de recul.
Notre 3ème discours se résume à ceci : (𓁝⇅⇆⊥𓁜)⇆𓂀, qui revient à ([⚤]⇅𓂀⇆[#]⊥𓂀)⇆𓂀. Graphiquement, cette équivalence⇆ revient à découper les deux lignes [#] et [⚤] du discours de 𓂀 et à les coller tête-bêche, pour former un ruban de Moebius.
- Tu avais déjà présenté une bande de Moebius dans l'article "Point #9-Symétries" :
/image%2F0964014%2F20201217%2Fob_f141a4_moebius.png)
- Sauf que sur ce ruban, le collage se fait dans l'autre sens: c'est le Symbolique du Sujet qui se colle sur l'envers du Réel.
- Nous revoici en pleine topologie !
- Tout à fait Thierry. Ceci va nous guider pour la suite.
(α)Puisque nous avons l'équivalence⇆: (𓂀⇆𓁝I𓁜)⇆𓂀, nous pouvons représenter l'espace du discours en [#]⊥𓂀 par deux axes orthogonaux :
| 𓂀/𓁝I𓁜 | ☯ | [∃] | [⚤] | [#] | [♲] | [∅] | ☯ |
| ☯ | (☯,☯) | (☯,☯) | |||||
| [∅] | |||||||
| [♲] | |||||||
| [#] | |||||||
| [⚤] | |||||||
| [∃] | |||||||
| ☯ | (☯,☯) | (☯,☯) |
Le discours en [♲]⇆𓂀revient à constater une équivalence redoublée :
ce qui revient à replier notre espace délimité par ces 4 points :
| (☯,☯) | (☯,☯) |
| (☯,☯) | (☯,☯) |
comme on ferme un mouchoir en nouant ses quatre coins. En topologie ça s'appelle "l'espace projectif", avec ici notre Auteur/Sujet à la place du point de projection.
Avoue que la figure finale de cet espace rapporté au point de vue♲ de l'auteur est assez élégante !
- À ceci près que ton espace projectif, que l'on peut représenter par la surface S2, ne renferme pas de volume S3 à cause de cette ouverture qu'est la place du Sujet au point de projection... Ton ballon de baudruche se dégonfle à cause de cette ouverture.
- N'est-ce pas toute la beauté de la chose ? Dès qu'il s'exprime, le Sujet se vide en se faisant auteur ! À mon avis, tu peux remplir une bibliothèque à partir de là...
- Mais arrivé à ce point final de notre représentation en ⇆𓂀 il faudrait malgré tout revenir sur Terre pour exprimer autre chose que de grandes généralités aussi intéressantes qu'inutiles comme "tout est dans tout et réciproquement" ...
- Bien sûr, mais il sera plus facile de retrouver notre chemin en repartant de ce point de projection.
1/ [♲]⇆𓂀 :
Nous retiendrons l'hypothèse que le principe d'équivalence♲, dans l'esprit de l'auteur [♲]⇆𓂀 a le même sens que celui qu'il prête au Sujet [♲]⇆𓁜.
- Mais peuvent-ils différer par leur connaissance des concepts de niveau [♲] ?
- À l'évidence. D'ailleurs, la définition des concepts à chaque niveau de notre Imaginaire diffère d'une culture à l'autre, et dans chaque culture subsiste des compréhensions différentes de [♲]. Cependant, et c'était notre axiome liminaire, la structuration générale du cerveau reste la même d'un individu à un autre, hormis sans doute certains cas pathologiques.
Tout ceci nous amène à dire qu'en écrivant ([♲]⇆𓁜)⇆𓂀, les deux signes ⇆ de part et d'autre des parenthèses ont le même sens.
2/ [#]⊥𓂀 :
Nous venons de voir que 𓂀 et 𓁝I𓁜 sont orthogonaux entre eux. C'est dire que le Sujet peut très bien tenir un discours sur celui qui se présente comme orateur. Lévi-Strauss observe les Jivaros, ce qui n'interdit nullement à ces dernier de se faire une théorie de l'Homme Blanc à partir de leurs observations de Lévi-Strauss.
Donc, le concept d'orthogonalité⊥ est le même au niveau [#] pour chacun de nos deux compères Dupont [#]⊥𓂀 et Dupond [#]⊥𓁜; et je peux écrire ([#]⊥𓁜)⊥𓂀, en gardant le même symbole ⊥ pour les deux (avec cette idée que ⊥𓂀=𓁜 et ⊥⊥𓂀=⊥𓁜=𓂀).
- Mais là encore, les deux niveaux [#] peuvent différer ?
- Oui et c'est là que c'est très intéressant : je peux situer mon Sujet 𓁝I𓁜 dans un espace hyperbolique en restant, moi qui en parle, bien au chaud et tranquille dans mon espace Euclidien familier ! Ce qui me permet de donner un sens à une représentation de ce type de l'espace relativiste :
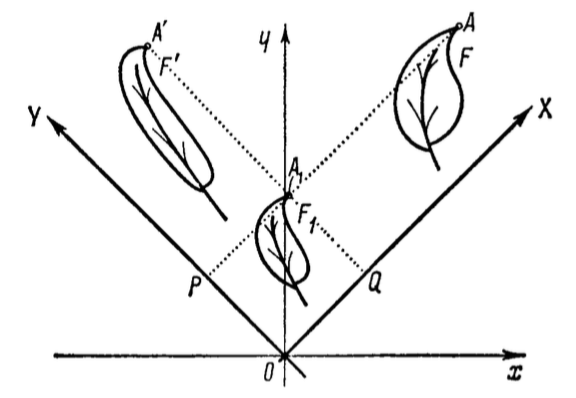
La seule chose que nos ayons en commun, c'est l'idée d'orthogonalité# !
Ça tombe bien, puisque ce concept d'orthogonalité# peut être ramené, comme nous l'avons vu avec la géométrie de Bachmann, (voir "Point #9-Symétries") à un principe de symétrie♲ de niveau [♲] !
Et du coup je commence à comprendre comment le petit mammifère que je suis, strictement conditionné par un cerveau qui se "voit" dans un espace Euclidien, peut s'échapper par la pensée et imaginer d'autres potentialités !
- Tu repenses à Bergson et ses "données immédiates de la conscience" ?
- Tout à fait, mais garde-le au chaud, nous y reviendrons sans doute...
3/ [⚤]⇅𓂀 :
Nous arrivons au niveau où notre Sujet 𓁝I𓁜 se délite ! Si par exemple, je parle de la relativité du temps entre ce que voit le chef de garde, fixe sur le quai 𓁜 et un passager 𓁝 en translation par rapport au quai, ils n'ont pas la même base de temps, il en est de même de l'auteur et du Sujet ([⚤]⇅𓁜)⇅𓂀 qui décrit l'un et l'autre.
- Attends un peu, chacun a malgré tout la même notion de successeur⚤, non?
- Certes, mais à ce niveau du discours, le temps est fondamentalement un concept diachronique qui s'évalue pour chacun d'eux par un décompte de sauts [∃]↑[⚤] qui lui est propre. Dans l'esprit de l'auteur [#]⊥𓂀, le temps de la narration est orthogonal# au temps qu'il décrit, de la même façon que dans l'esprit du Sujet [#]⊥𓁜, l'espace et le temps sont orthogonaux#.
Je comprends la chose ainsi :
C'est pourquoi, lorsque j'écris (𓁝⇅[#]𓁜⏩𓁝[#]⊥𓁜)⇅𓂀, le symbole ⏩ est utilisé pour représenter la succession dans la narration⇅ de 𓂀 qui se distingue d'un temps propre au Sujet [⚤]⇅𓁜, symbolisé par ⇅.
- Mais peux-tu avoir deux bases de temps sans commune mesure dans un seul discours ?
- Oui, dans la mesure où au niveau [#]⊥𓂀 nous avons déjà vu que les Imaginaires de l'Auteur et du Sujet sont orthogonaux ! Nous en tirons ici la conséquence au niveau le plus primitif du discours :
Le temps de la narration⚤ est orthogonal# au temps⚤ du Sujet dans le discours.
- Ce qui te permets de retomber sur tes pattes !
- À mon grand soulagement !
En résumé
1/ En ayant à l'esprit que "Je est un Autre", on forme l'hypothèse que la structure Imaginaire de l'auteur du discours est semblable à celle du Sujet dont il parle.
☯[∃] [⚤] [#] [♲] [∅]☯
2/ Les concepts de similitude♲, d'orthogonalité# et de successeur⚤ sont commun aux niveaux respectifs [♲], [#], et [⚤] du Sujet 𓁝I𓁜 (dans le discours) et de l'auteur 𓂀 (chapeautant le discours).
3/ Le concept commun d'orthogonalité# permet d'articuler une expression euclidienne (pour 𓂀) d'un espace non-euclidien (pour 𓁝I𓁜).
4/ Le concept commun de successeur⚤ permet à l'auteur 𓂀 de décrire des évolutions du Sujet 𓁝I𓁜 dans un "temps narratif" (i.e.: symbolisé par ⏩) , décorrélé du temps propre au Sujet (i.e.: symbolisé par ⇅).
- Si l'on garde bien ceci en tête, l'expression (𓁝⇅[#]𓁜⏩𓁝[#]⊥𓁜)⇅𓂀 (1) qui nous avait fait tiquer garde un sens : le Sujet peut être décrit à un niveau [#]𓁜 de son Imaginaire, par un auteur qui en reste au niveau [⚤]𓂀 du sien pour la simple raison qu'il s'agit d'une coupe par le niveau [⚤]𓂀 d'un discours plus complet s'exprimant sur deux axes orthogonaux# dans l'Imaginaire de l'auteur...
- Ouf !
Hari (α)