Retour sur le point de capiton - Les transformations naturelles

- Comme tu le sais, je suis routinier, et chaque matin je lis les statistiques de ce blog, comme d'autres leur horoscope dans l'espoir de trouver l'âme soeur, celle qui comprendra enfin l'importance de mes divagations.

- Et la pêche est bonne?

- Désespérante mon ami. Fort heureusement, je n'ai pas le goût du désespoir! Passons. Il y a deux jours donc, je vois que ma présentation au groupe de logique catégorique du 12/06 dernier a été lue par quelques-uns, ce qui me donne l'envie de la relire.

Et j'ai tout d'abord la satisfaction de constater que tous mes développements depuis lors s'enracinent bien là, ce que je confirme en ajoutant quelques commentaires, jusqu'à ce que j'arrive au point 3/ abordant "les transformations naturelles", que j'illustrais par ce schéma:

Soit:

• 2 catégories C et D;
• 2 foncteurs F: C→D et G: C→D;

Une transformation naturelle η de F→G est la donnée pour tout X de C de η_x : F(X)→G(X); telle que pour tout X et Y de C ainsi que pour tout morphisme f de C le diagramme commute: 

η contravariant	η covariant

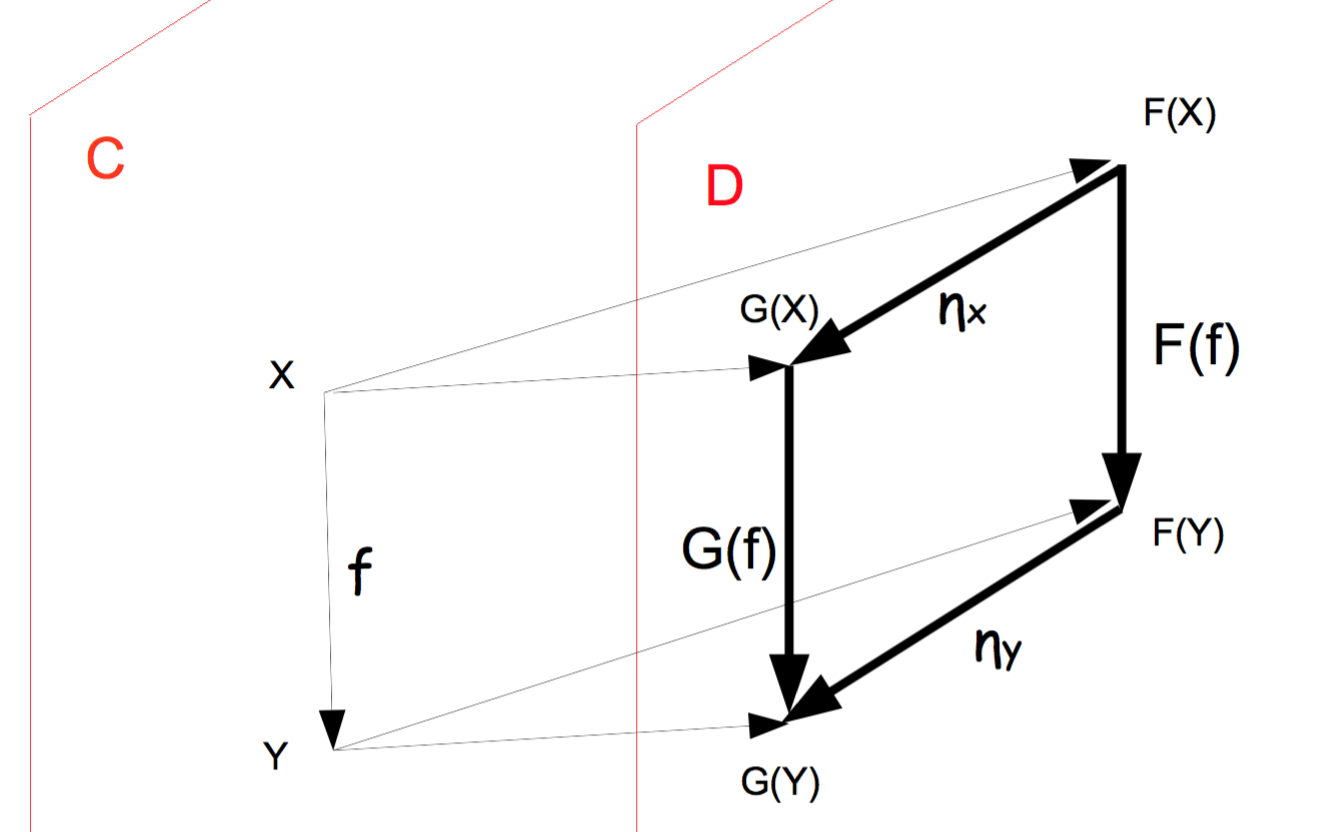fig. 3

Or, à l'évidence, le diagramme de gauche ne commute pas ! 

- C'est-à-dire, pour les non-matheux ?

- Tu vois bien que pour η covariant, je peux passer de F(X) à G(Y) soit en enchaînant les morphismes G(f).η_x, soit par η_y.F(f), tandis que mon schéma coince pour η contravariant!

Autrement dit, j'ai écrit une connerie et personne n'a moufté... C'est-à-dire que mon auditoire avait déjà décroché à ce moment de ma présentation ! Triste constat, mais passons.

J'ai donc modifié mon article avant-hier avec les schémas suivants :

η contravariant	η covariant

fig. 3 bis

Ce qui a posteriori est évident ! Et depuis deux jours, je cherche à comprendre la cause de cette erreur qui me surprend.

- C'est important?

- Cette erreur est un symptôme, et comme en l'occurrence je suis l'analyste en 03/20 de l'analysé de 06/19, j'ai ma petite idée quant à sa cause.

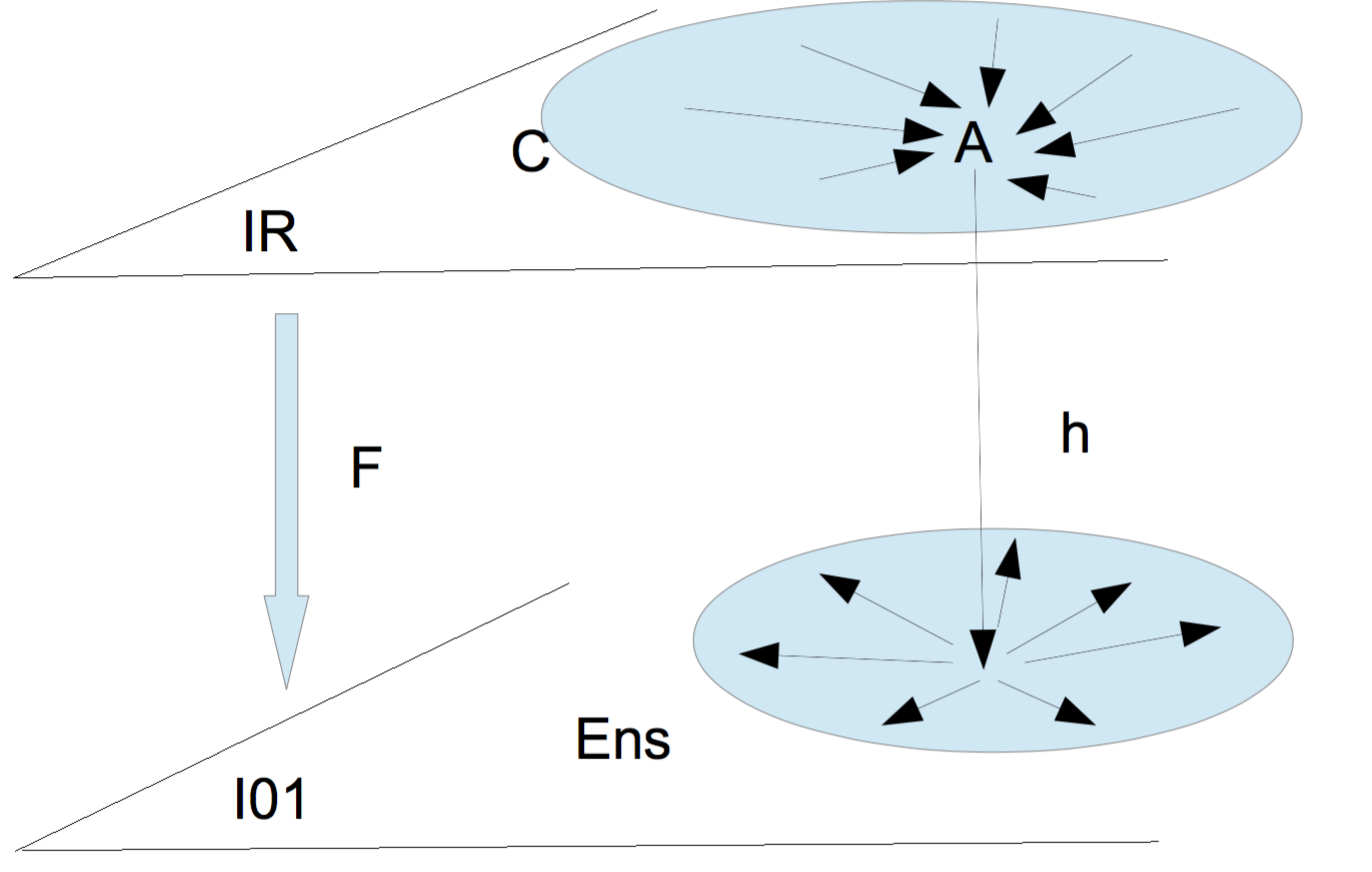
Reporte-toi à mes schémas représentant foncteurs covariants et contravariants:

• F est dit covariant : lorsque A est le domaine commun de Â;
• F est dit contravariant : A est le codomaine commun de Â.

 =Hom (- ;A) : X⟼Hom (X ; A)	 =Hom (A; -) : X⟼Hom (A ; X)
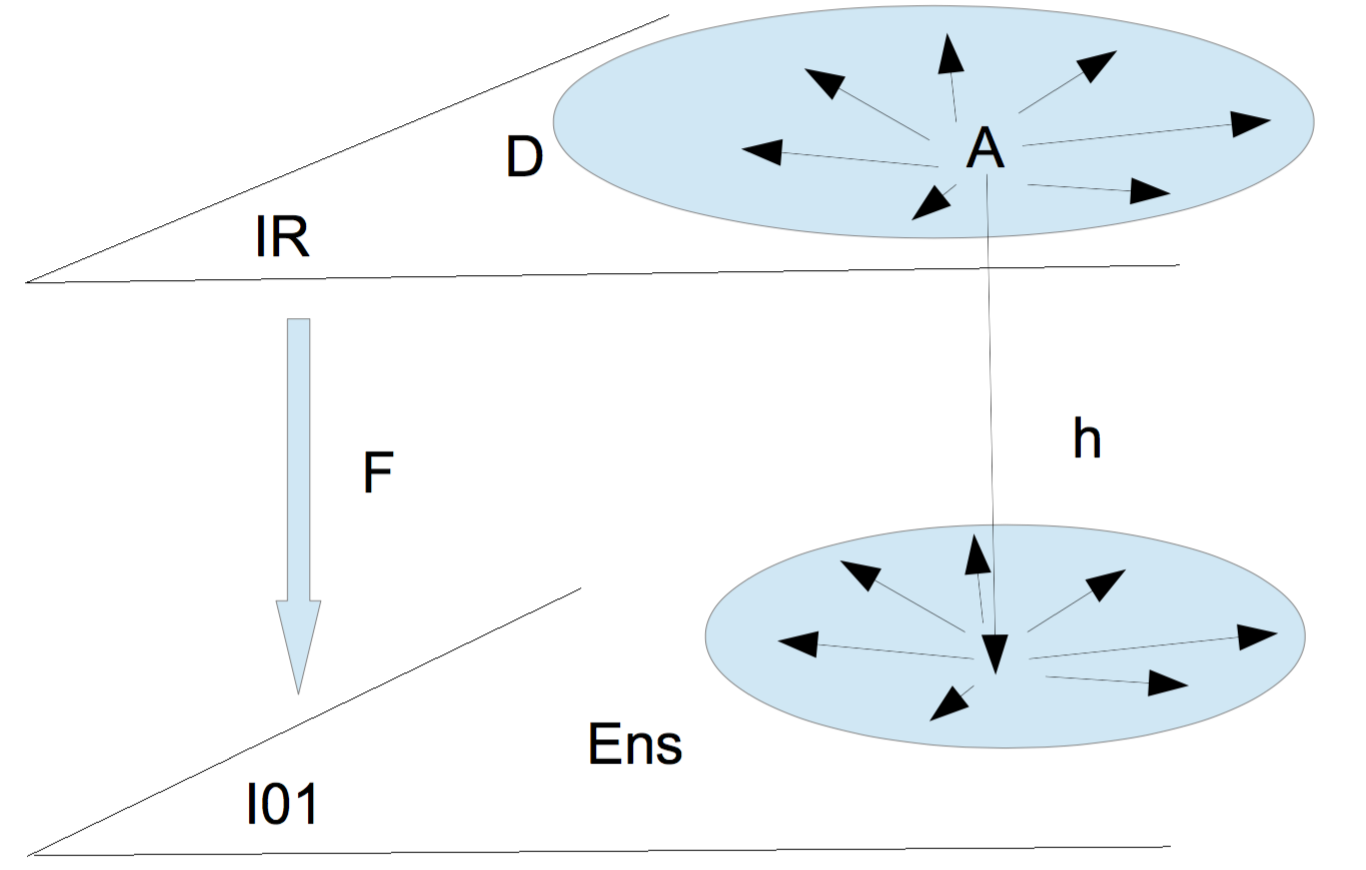F contravariant	F covariant

fig. 2

En tournant mes deux faux schémas de la fig. 3 d'un quart de tour sur la gauche, tu vois que la catégorie C de la fig.3 colle avec la catégorie Ens de la fig.2. Autrement dit, j'ai le préjugé implicite que C est "naturellement" le codomaine de mes Foncteurs F et G, alors que je pars explicitement de la définition inverse ! 

J'ai donc un blocage !

Si maintenant je tourne mes schémas de la fig.3bis de 1/4 de tour sur  leur droite, c'est alors la catégorie D qui colle à la catégorie Ens de la fig.2, autrement dit, mon schéma commutatif en D définissant η est de niveau Imaginaire I01, et non IR., et l'ensemble est cohérent.

J'avais bêtement préjugé d'une complexification progressive des concepts, et dans cet ordre d'idées, la transformation naturelle devait se situer "au-dessus", du concept de foncteur. C'est une erreur fondamentale, liée à l'idée, très cartésienne, que nos concepts se construisent dans un processus purement immanent, par strates successives. 

Or, dès que l'on dépasse le niveau Imaginaire I01, l'automatisme de répétition qui nous fait sans cesse utiliser un même processus n'est plus de l'ordre de la succession mais de l'orthogonalité !

- Explique-toi !

- Je comprenais à l'époque le foncteur F↓, concept diachronique entre I01/IR comme la dégénérescence d'un concept synchronique F→ ou F← au niveau IR, répétant le schéma d'où j'étais parti, selon lequel le morphisme f↑ est la dégénérescence entre I1/I01 d'un concept synchronique f→ ou f← au niveau I01.

Ces dégénérescences univoques soit  f↑, soit F↓ étant d'une certaine façon des brisures de symétrie ←/→ conceptualisées ex post, au niveau I01<Im pour le morphisme f et IR<Im pour le foncteur F.

J'ai tourné mon schéma de 90° pour, dixit, "un confort de lecture". C'était un prétexte, car en réalité, j'étais mal à l'aise à l'idée de représenter un foncteur F: C↑D, alors que je venais de discuter de foncteurs "représentables" descendants F:C↓Ens. En écrivant F:C→D horizontalement, j'esquivais le problème grâce à cette rotation ad hoc.

Or, cette crainte n'avait pas lieu d'être car dans une approche topologique, je peux concevoir les deux mouvements ↑ et ↓ entre deux niveaux Ik et Ik+1:

• Un "mouvement" ↑ (i.e.: soit foncteur, soit morphisme) ascendant de Ik vers Ik+1 est vu de Im, avec Ik<Ik+1<Im, dans une posture logique qui reste le point de vue global  de la pensée topologique,
• Un "mouvement" ↓ vu de Im comme globalement descendant de Ik+1, reste localement ascendant ↑, vu en miroir relativement à I'm dans l'approche topologique : I'm<Ik<Ik+1<Im. Autrement dit, l'avatar I'm de Im "singe" localement une pensée logique -il fait "comme si"- lorsqu'il oriente son regard vers I0, par dessus l'épaule de Im.

C'est cette dualité ↑↓ que je n'avais pas encore parfaitement maîtrisée à l'époque, et sur laquelle je suis revenu dans mes derniers articles, à partir de mes réflexions sur "La propriété universelle en théorie des catégories".

À l'époque de cet article, j'étais encore dans une approche très "logique", obnubilée par l'aplatissement ←/→ en I01 de morphismes ↑/↓ entre I1/I01, et par la réification de tout mouvement en concept synchronique, plat. Mais cette idée est typiquement une conception logique des choses, dans laquelle l'automatisme de répétition mène au concept de successeur.

J'avais bien noté qu'au-delà de I01, l'automatisme de répétition n'est plus de l'ordre de la succession, mais de l'orthogonalité, sans toutefois y astreindre ma propre pensée.

- Tu peux préciser pour ceux qui sont largués?

- En I01, l'automatisme de répétition, représenté par le concept de successeur, conduit à construire la suite des entiers naturels où n+1 est le suivant de n; tandis qu'en IR où, de l'ensemble N puis Q, tu passes à celui des nombres réels R (avec l'hypothèse du continu), la répétition du saut te mène à R² ou C, puis R³ etc... Autrement dit, de la droite, tu passes au plan, puis au volume et ainsi de suite.

Et bien, dans mon obsession de "tout aplatir", j'avais mal compris la nécessité de conserver, au-delà de I01, cette "orthogonalité". Dans mon texte, Je constatais bien le passage d'une écriture linéaire en 1D à des schémas en 2D, mais sans réellement comprendre ce dont il s'agissait.

- As-tu évolué depuis?

- Je crois que oui, depuis mes dernières réflexions quand à la place relative du Sujet et de l'Objet (voir: V.I.T.R.I.O.L.).

En fait, il ne s'agit pas tant d'une différence essentielle entre concepts synchronique et diachronique, que d'une différence relative à l'attention du Sujet, portant tantôt sur l'objet, tantôt sur sa propre situation par rapport à l'objet.

Par exemple, le miroir, dans la phase dite du miroir chez Lacan, peut être soit:

• Un "objet synchronique", que je peux décrire ici et maintenant, lorsque je focalise sur lui mon attention, et je suis alors l'agent "diachronique" de ma vision,
• Un "agent diachronique" entre Im et I'm lorsque grâce à lui je prends conscience de mon image.

Ce qui compte, dans la représentation du mouvement, c'est l'orthogonalité entre synchronie et diachronie, qui se conserve même lorsque je change de focale, si je puis dire.

- Tu nous emmènes bien loin de nos transformations naturelles !

- Pas tant que ça. D'ailleurs ce terme de "transformation" me semble fort bien trouvé, car il garde en lui cette idée de mouvement, autrement dit la nécessité d'une orthogonalité entre deux concepts, l'un ↑/↓ et l'autre ←/→, sans préciser plus avant lequel est "synchronique", lequel est diachronique.

La brisure de symétrie intervient lorsque je représente un foncteur en le "ramenant" en Ens (i.e.:  F: C↓Ens, représenté par le morphisme h:C↓Ens).

Comme vu précédemment, l'effet "miroir" de I01 renvoie face à face :

• Une brisure globale de symétrie en dessous de I01, portant sur un concept synchronique ←/→, dégénérant en ↑, vu de I1<I01<Im
• Une brisure de symétrie au-dessus de I01, portant sur un concept diachronique ↑/↓ rapporté à Ens en I01,
  • vu localement comme ↑, avec I'm<I01<IR;
  • vu globalement comme ↓, avec I01<IR<Im.

- Tout ceci me semble bien compliqué !

- J'en suis désolé, mais le repérage précis du Sujet dans son propre discours est à ce prix. Ça demande un peu d'entraînement pour se sentir à l'aise dans l'exercice, et encore ! Cette erreur, que j'ai repérée tardivement, montre que je suis loin d'être virtuose en la matière !

Il me reste à relire la fin de cette présentation, pour voir si ce recadrage me permet d'y gagner en clarté !

Le 11/03/2020

Pour la suite, nous poursuivrons à partir des schémas définitivement (je l'espère!) redressés suivants :

η contravariant	η covariant

fig. finale

Ces schémas permettent de mieux repérer la nature covariante/ contrariante de nos foncteurs F et G; et gardent leur pertinence lorsque les concepts dégénèrent et que D se limite à la catégories Ens, en I01 (i.e.: en abandonnant l'hypothèse du continu qui caractérise IR), en respectant visuellement  la stratification Imaginaire Ens∈I01<C∈IR.

Tu remarqueras que notre représentation en 3D illustre bien l'orthogonalité fondamentale qu'il y a entre :

• La transformation naturelle η;
• Les foncteurs F et G;
• Les morphismes f, F(f) et G(f).

Pas de quoi s'en étonner, puisqu'au-dessus de I01, la répétition du même conduit à des concepts orthogonaux entre eux. Or, le foncteur est un "morphisme de morphismes", et la transformation naturelle un "foncteur de foncteurs".

- Cependant, tes schémas sont plutôt de projections 2D d'un objet 3D, ce qui pose la question de  savoir de quel point de vue ces projections sont l'expression.

- Excellente question !

Si je voulais expliciter tout le contexte du schéma, il est clair que j'arriverais à notre feuilletage Imaginaire habituel, I1<I01<IR<I#<I0, encadré par le Réel et le Symbolique, avec Im et son avatar I'm se glissant entre les feuillets au grés du Sujet.

- Ça, nous le savons depuis fatigué ! 

- Oui, oui, mais ta question m'a fait prendre conscience de quelque chose que je voudrais t'amener à comprendre par toi-même ! Et pour cela, il m'est venu l'analogie suivante, que je reprendrai certainement assez souvent à partir de maintenant.

Représente-toi le Sujet comme un livre dans lequel :

• La 1^ére de couverture serait le Réel,
• Les 5 pages du livre seraient I1,I01,IR,I#,I0,
• La 4^ème de couverture serait le Symbolique.

Ensuite, il convient de comprendre de quelle façon le Sujet « prend conscience de lui-même ». Dans notre métaphore, il découvre son propre Imaginaire au fur et à mesure qu'il lit ce livre le représentant. Ce qui nous conduit à situer son état de conscience actuel, à l'aide d'un marque-page Im glissé après la dernière page lue.

En suivant J. P. Changeux nous dirons que le Sujet prend conscience d'un objet quelconque lorsqu'il rapporte un percept, montant du Réel, via ses yeux, ses oreilles, ou tout autre sens, à un concept, déjà acquis et présent dans son cortex.

La dernière page en dessous de ce marque-page indique son «niveau de conscience», ce qui est au-dessus de lui formant, pour nous qui tenons le livre en main, son «inconscient», autrement dit ce qui échappe au Sujet dans la posture indiquée par le marque-page.

Comme tu le vois, le Sujet ne peut utiliser pour se représenter lui-même que le vocabulaire à sa disposition à cette étape de sa lecture, c'est-à-dire, les premières pages du livre, celles qui précèdent le marque-page Im.

Pour suivre l'évolution psychique du Sujet, il nous suffit maintenant de l'accompagner dans sa lecture et de  «tourner avec lui les pages» de ce livre, de la première, jusqu'à Im.

Tu auras compris que la page I01 de notre livre Imaginaire est comme un miroir, grâce auquel notre marque-page Im reconnait son reflet I'm, comme un avatar de lui-même, situé entre les pages I1 et I01.

Nous dirons que le Sujet dédouble son point de vue et qu'il peut à sa convenance adopter :

• Soit un point de vue global, vu de notre marque-page Im, que nous avons défini comme «rationnel logique»
• Soit un point de vue local, vu de cet avatar I'm.

- Oui, je vois que tu te fais plaisir en délayant la sauce, mais où veux-tu en venir ?

- À cette question : où se situe celui qui tient le livre ?

- Tu y as déjà répondu : c'est ton démon de Maxwell, ton DM hors discours : R<I<S<DM.

- Certes, mais je l'avais situé sur mes schémas au-dessus de S, dans l'alignement diachronique général R<I<S, ce qui implicitement le pose dans cette hiérarchie qu'il tente de décrire ! Et là encore, cela montre que je restais dans une pensée cartésienne, m'appliquant à démonter les rouages d'un mécanisme pour le reconstituer étape par étape.

- Mais où est-il, alors ?

- Tout ce qu'il faut retenir, c'est qu'il n'est pas partie prenante de sa description, autrement dit, que ce discours lui est "orthogonal".

- Quel rapport avec ton livre ?

- Je tiens mon livre comme bon me semble, sans que mes manipulations interfèrent en quoi que ce soit avec ce qu'il contient: DM n'est pas "au-dessus" du Sujet, il lui est étranger, comme l'axe des abscisses est étranger à celui des ordonnées.

Et, pour en revenir à nos schémas, ce sont les projections 2D d'un objet en 3D construit selon 3 dimensions orthogonales entre elles :

• morphismes
• foncteurs
• transformations naturelles

Et je (en DM) fais ces projections, pour illustrer au mieux la dégénérescence possible de cet objet lorsque je "représente" une catégorie C par un foncteur F: C↓Ens.

Si donc, je suis sur une 4ème dimension par rapport à cet objet 3D, je peux rester orthogonal à mes projections tracées en 2D sur une feuille, en me situant dans l'espace ordinaire 3D, hors de cette feuille, pour que mon regard en la surplombant puisse la voir, avoue que ça tombe plutôt bien ! 

Hari