An "entropological" approach of mathematical "categories" #3

This article follows the previous one #2 where we commented the concepts of "object", "map" and "rule". We saw that the mathematical "categories" respect what we consider as the two first elementary axioms of any language:

• the "dichotomous" principle : at its lowest level any language is structured upon simple pairs of antagonists concepts such as 0 / 1;
• the "non contradiction principle".

This conducts to discriminate the "domain" A and the "codomain" B.

But what is happening when we consider A two time, one as the domain and the other one as the codomain, regarding this particular rule : for every a of A (domain), then a => a of A (codomain) ?

Identity map

Consider a general relation f between A and B, where A and B are defined each one at an Imaginary level (respectively IA and IB). Then, in order to imagine a rule f between A and B, we have to go upstream the "diachronical axis" of our Imagination, in order to define a level IAB, where we can Imagine together A, B and the rule f itself (i.e.: in order to consider them in a same synchronical discourse). A good metaphor would be the sheet of paper we use to describe this operation by a drawing: we need to choose a sheet of paper, before we start our drawing; even if, after all, we don't take care of this sheet. Obviously, this sheet is the hidden support of our representation. As well as, during my walk on a road under the sun, this road is the implicit support of my shadow. I need always a surface in order to consider any"map".

Now, what can we say, considering this rule : for each a of A, then a of A.

In first, I need to realize the same gap IA => IAB as previously, in order to Imagine several sets aside, on the same map. It can be whatever type of set, such as our previous B or A itself, in the present case.

Formaly, we have to do the job two times: the first gap to erect A as a domain, and the second, as a codomain.

It is important to consider this very closely: if I do actually this 2 gaps between IA and IAB, we saw (refer to the previous article) that implies some time to do this, with a certain undetermination...

Consider as an example a sentence like this one: I speak french as well as Napoleon. I assume that "french" refer to the same language. But is it really true? Obviously not: our vocabulary is not the same, and the grammatical rules have changed between 1800 and 2016. And this evolution, this change in the language is, in the original sens of the term, a "diachronical evolution".

In fact, I can avoid such "time consideration" because I have not to do those 2 gaps: one is enough. Because the characterization of A as a domain or a codomain is typically a consideration regarding the IAB level, the level where is defined our map. I have just to remain the diachronical gap between IA, where I have no idea of what is a map, and IAB, where I construct this particular object (in the sens the theory itself gives to the term "object") : a map.

But, even in that simple case, avoiding time consideration, can I say that A at IA level remains unchanged at IAB one ?

Consider that our A is a baby named Charly, and try to imagine what is "Charly" for himself. In child development, mirror stage is where the ego is born. Let's define the Imagination level of Charly, before he reaches this "mirror stage" as Im-1, and Im, the level he reaches after he recognizes himself as a whole. Can we say that Charly is the same in Im-1 and after he reached the level Im ? Obviously not, because in that case, he changed his position from ex-ante to ex-post (please refer to : "Le stade du miroir"), and he constructs the object "Charly" for himself in the time he makes this diachronical jump.

You could object that the case is not relevant, because the object A doesn't exist at the level Im-1. So let's consider an unanimated object such as "light". And consider the 2 imaginary level:

• Ic, where we consider the elementary photons;
• Iw, where we consider the light as a wave.

Can we consider that the concept "light" remains unchanged when we change our mind from Ic to Iw? Obviously not (please refer to the article "onde et corpuscule").

Those examples are sufficient to say that, in our ordinary experience, the "objects" of our attention (depending of our intention) are related to the Imaginary level where we consider them.

But not here : in the mathematical language, we don't take in consideration any modification of the object, either due to the time (an evolution) or to a pure "diachronical gap" as seen on our previous examples. Mathematics is purely a "synchronical language". And we assume that A remains unchanged when we change our Imaginary level. And this is a major issue in mathematics. In geometry, for example, a figure remains unchanged, when we modified the the base of its coordinates...

We have already discussed about the meaning of X1 or "one time" in my article "regard entropologique sur les maths suite 1" and we concluded that this neutral element (for the multiplication) is a pure "diachronical jump".

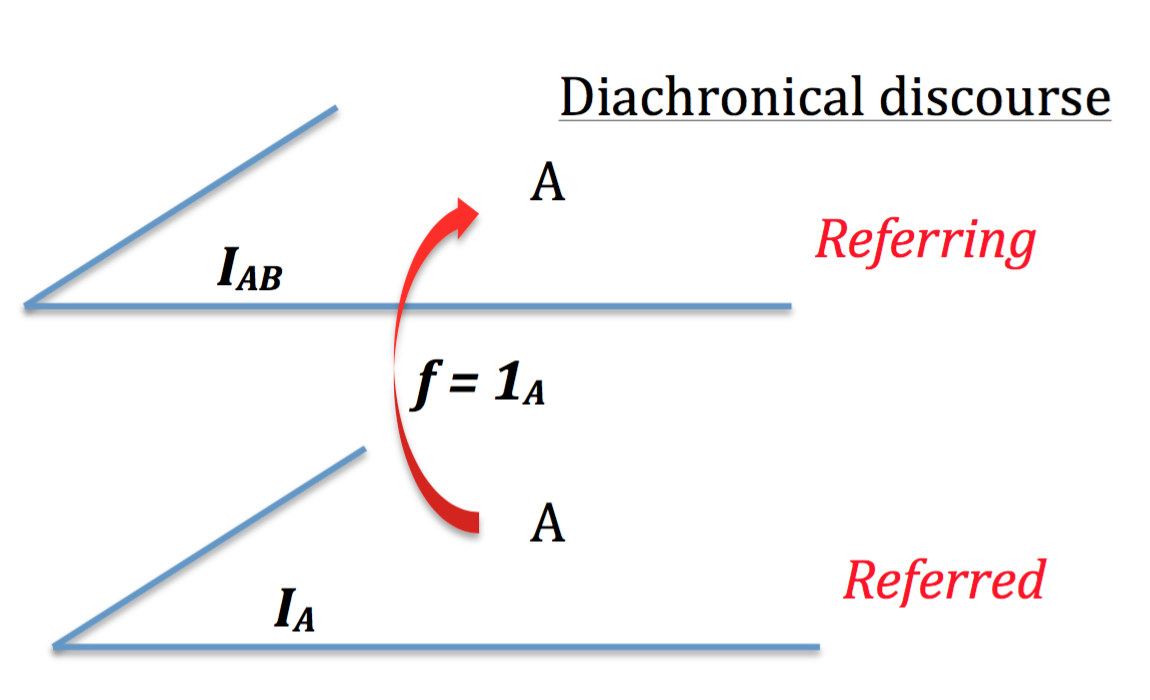
Let us use the terms of the linguistic to express the elementary action of using the term "A" in order to start the description of a map, referring to a set "A", which is described at a lower level of my Imagination, i.e.: before any idea I could have regarding the rules to define a map. I can say that the term "A" I use to define my map (at a level IAB) is referring to a set "A" (at the level IA):

• "A" at IAB level is the referring object;
• "A" at IA level is the referred object.

And this elementary action that I am doing, can be described, as usual for any "motion" or "action" by the use of a diachronical concept linked to a synchronical one. You can see it represented on the following drawing, represented by 2 red arrows:

• the first one is a pure diachronical jump; it is the projection of the referred term A at IA level, to the place of the referring term A defined as the domain A at IAB level
• the second one is an expression, in the IAB synchronical language of an identity between the referred object represented by "A-domain" and the referring object represented by "A-codomain".

In others mords, the fonction identity 1A is a representation ex-post (at IAB level) of a motion involving a synchronical concept A (at IA level) and a diachronical concept between IA and IAB levels.

And the mathematical language, purely synchronical, doesn't represent the motion, but only a trace after its achievement.

=> That is why, the reverse action IA-1 can only be defined if IA exists.

As a matter of fact, after we have reached the IAB level and defined A as a domain of the map, we can't deconstruct this. To imagine A as a codomain, implies obviously that we have already done the jump between IA and IAB.

I suggest to summarize those remarks about the identity relation, as follows:

1/ in a upstream diachronical jump, an object A is not changed :

=> A at IA level = A at IAB if IA < IAB this is the relation identity noted : 1A

2/ If 1A exists (i.e.: that means A exists at IA level) then

=> referring A = referred A <=> A-domain = A-codomain :

=> and then 1A = 1A-1

The interest of this point of view is to connect the mathematics language to a more general approach, taking into account a very basic definition of the time as a "diachronical jump", and any motion as a dual concept involving 2 concepts:

• One diachronical concept (as the time)
• One synchronical concept (as the space)

An approach where we find the two different ways we used to represent a motion:

• Either we describe the motion itself, with a synchronical concept at Ik level and an associated diachronical concept between Ik and Ik+1 level, (example space at Ik and time between Ik and Ik+1) and we are in the action, during its fulfillment; while the motion is on progress,
• Or we describe the result of the motion (ex post) by a synchronical concept at the upper level Ik+1 (example : speed at Ik+1); but we are disconnected from the scene, not any more like a spectator or an actor, but like a film critic, at a higher position on our diachronical axis.

The rising question, now, is to understand how we can describe a physical motion with this mathematical language which evacuates any consciousness of time (all well as any uncertainty during a motion) by this axiom of identity.

Nevertheless, at this stage, I can say that there is no contradiction between our "entropological" approach are those very elementary concepts of the mathematics, at the lowest stage I can imagine...

To be continued...

Hari