Le point #9 - Symétries

- Pour préparer cette présentation au groupe CLE, j'ai beaucoup repensé à la démarche Galoisienne, sans en être complètement satisfait. Je n'ai pas ressenti ce déclic qui me permettrait de dire que j'ai parfaitement compris, pour passer à autre chose.

- Qu'est-ce qui te chagrine ?

- Je bute sur cette propriété d'un sous-groupe distingué, en [⚤]𓁜, que je voudrais rapprocher du va-et-vient entre identité et idempotence que l'on retrouve en topologie 𓁝[#]𓁜.

J'ai compris que c'est lié à un principe extrêmement profond, qu'Emmy Noether a établi au niveau le plus élevé, le plus général de l'entendement humain, tout au moins jusqu'à nos jours, en [♲]𓁜  sous forme d'un triptyque qui s'exprime ainsi dans notre jargon :

• L'apparition d'une symétrie (i.e.: dans un saut diachronique ↑), plus facilement repérable par une rupture de symétrie  ↓;
• Se traduit par une quantité conservée (i.e.: repérée ex post par 𓁜);
• Est accompagnée d'une indétermination (i.e.: par définition d'un saut diachronique ↑)

Prends un exemple simple : la loi d'inertie de Galilée.

• La vitesse d'un mobile soumis à aucune force est constante dans un repère Galiléen => v=quantité conservée en  [♲]𓁜 ;
• La rupture de symétrie de la vitesse se constate en [#]𓁜 où  elle est éclatée entre temps⊥espace ;
• Le passage de [#]𓁜⏩[♲]𓁜 est entaché d'une indétermination: c'est le principe d'incertitude d'Eisenberg.

Il s'agit à mon sens d'un principe absolument universel, qui tient à notre façon actuelle de penser hic et nunc, et donc je m'attends à en retrouver la trace dans les travaux de Galois.

- Nous sommes bien d'accord qu'il s'agit de ton regard, nécessairement rétrospectif, sur des travaux d'il y a deux siècles ?

- Évidemment, mais je prétends que Galois est en rupture avec une épistémè occidentale héritée de Descartes, et qu'aujourd'hui encore, notre mode actuel de penser, post-cartésien, trouve sa source en lui. Je fais de l'archéologie, dans les traces de Foucault.

Pour en revenir à Noether, comme tu le vois sur notre exemple, une symétrie serait donc quelque chose de repérable en [♲]𓁜 par une conservation, se traduisant par l'apparition d'une orthogonalité dans le saut régressif ↓ en [#]𓁜.

Mais Galois nous tire vers le bas, en exprimant les symétries au niveau [⚤]𓁜 grâce à la théorie des groupes.

- Je vois à peu près, mais que vient faire ici le couple identité/ idempotence ?

- Nous en avons déjà beaucoup parlé (note 1) :

• En position rationnelle logique [∃][⚤]𓁜, le Sujet identifie l'objet final (*)↑{1} et toute identification dans cette position se ramène à ce schéma originel.
• L'idempotence tient à une perception locale ex ante d'un objet, c'est typiquement lié à une approche locale topologique 𓁝[#].
• Toute la discussion topologique tient à une bascule 𓁝[#]𓁜, autrement dit aux concepts de section/ rétraction. (c)

Le concept d'identité, très simple dans une approche rationnelle logique, devient plus complexe en topologie !

1. Là où un unique saut [∃]↑[⚤] suffisait à identifier en [⚤]𓁜 un "objet" repéré en [∃]𓁜,
2. le Sujet est écartelé entre une posture ex ante (locale) 𓁝 et ex post (globale) 𓁜 autour d'un "objet" qui se repère en [#] avec 𓁝[#]𓁜.

Encore ces identifications ne sont-elle pas de même nature :

1. Dans le saut [∃]𓁜⏩[∃]↑[⚤]𓁜, le Sujet repère l'objet référé en [∃] par son étiquette en [⚤] : l'objet est vu comme élément discernable d'un ensemble ;
2. En 𓁝[#]𓁜, l'objet référé n'est qu'un élément indiscernable d'une partie d'un tout, qui seule est identifiable. Le Sujet ne peut qu'étiqueter cette partie et non l'objet lui-même.

Pour restituer la question dans la perspective générale que j'ai indiquée en préambule :

"L'objet vu comme "élément d'un ensemble", dans une posture [∃][⚤]𓁜 semble rompre la symétrie existant entre les "éléments d'une section" dans une perspective topologique 𓁝[#][∅]."

Cette vision proprement topologique 𓁝[#], se traduit algébriquement en [⚤]𓁜 en termes de groupes quotients, dans un mouvement   [⚤]𓁝𓁜[#]⏩[⚤]𓁝𓁜[#].

- Tu nous éloignes...

- Il faut prendre du recul pour apercevoir un point de fuite à l'horizon.

Revenons sur cet aller-retour section-rétraction et note la rétraction comme π pour "projection" et la section comme π^-1, et tu vois une différence entre l'enchaînement des opérations π°π^-1=1_A et π^-1°π=e, se traduisant par une différence dans l'ordre de l'enchaînement des opérations !

Nous avons dans l'écriture une différence droite-gauche, qui se représente également au niveau plus élémentaire [⚤]𓁜, et donc :

Une différence identité/idempotence en 𓁝[#]𓁜 est repérable en [⚤]𓁜 par une différence algébrique entre  opérateurs "à droite" et "à gauche".   

Je crois qu'il faut prendre le temps de bien assimiler la différence entre les points de vue ex post 𓁜 et ex ante 𓁝, à partir d'un enchaînement de saut ⇅ : (b)

• Entre [∃]𓁜 et [⚤]𓁜, un saut ↑ est l'identification (*)↑{1}, et le saut inverse ↓ ne peut que tu conduire à l'objet final {1}↓(*) : c'est la propriété universelle de la théorie des catégories, et la répétition ⇅ n'amène aucune variation ;
• En 𓁝[#]𓁜, l'enchaînement 𓁝↑𓁜⏩𓁝↓𓁜 conduit à I_A, quand l'enchaînement contraire 𓁝​​​​​↓𓁜⏩𓁝↑𓁜 conduit à e, autrement dit, tu passes d'un élément à l'autre d'une même section. L'enchaînement des opérations ⇅ conduit donc à explorer au hasard l'ensemble des éléments d'une section.

C'est là sans doute qu'il faudrait comprendre la régression [⚤]𓁝𓁜[#]⏩[⚤]𓁝𓁜[#], autrement dit le l'expression algébrique de ces opérations ⇅ en [#], comme le premier groupe d'homologie d'un objet, limité à ces points. Dans cette perspective, les "points" de l'objet en sont le bord extrême, lorsque d'une vision topologique 𓁝[#] de l'objet je passe à sa description algébrique [⚤]𓁜.

- Comme tu définis le corps de base en [⚤] d'un espace vectoriel en [#]?

- Tout à fait, mais, comme je veux retrouver les principes de Noether, j'élargis ma vision du problème en tentant de raccorder tout ceci aux groupes d'homologies (note 2).

- Quitte à élargir ton champ de vision, brosse-nous un tableau d'ensemble nous permettant de suivre ton discours.

Homologie, topologie, géométrie et algèbre :

- Tu as raison : commençons par la fin, et donc par moi 𓂀 qui tient ce discours. Au fil des développements que tu peux suivre sur ce blog, tu as pu te rendre compte du mal que j'ai à dépasser le mode de penser cartésien, et je me suis surpris plus d'une fois à pointer une dissonance cognitive à cause de cela; tentant d'expliquer en position [⚤]𓂀 la posture du Sujet en [#]𓁜. Cependant, je pense avoir une idée assez claire du niveau [♲]𓂀, autrement dit, c'est ma vision intermédiaire [#]𓂀 qu'il me faut encore travailler.

Je pense que ma difficulté essentielle tient à ma façon instinctive de comprendre la répétition du "même" comme une succession de sauts ↑, autrement dit en termes de catégories, une succession de morphismes dans la position rationnelle logique  [∃][⚤]𓂀. Je sais, par la raison, que la répétition du même au niveau supérieur, entre [⚤] et [#], se traduit par une orthogonalité entre concepts, dans la position [⚤][#]𓂀. J'ai beau le savoir, mon esprit est à la traîne... Je ne suis pas le seul, note-le bien.

- Attends un peu : si tu ne vois pas ce niveau [#]𓂀, ni personne d'ailleurs, qu'est-ce qui te permet de présumer de son existence ?

- C'est comme une pierre laissée par un gamin sous un chapeau : tu n'en prends conscience qu'en donnant un coup de pied dedans ! La douleur en t'éveillant t'amène à penser qu'elle avait une cause objective quoiqu'invisible.

- Mais encore ?

- Il y a une difficulté à définir une figure géométrique dans un langage séquentiel, et d'une manière générale à passer du continu au discret, et "mettre de l'ordre" dans une figure. Cependant, et cela peut paraître paradoxal, nous manions quotidiennement les objets de notre environnement à l'aide de concepts de niveau très élevé. Je suis incapable de te définir correctement une patate, cependant je n'ai aucun problème pour en acheter un kilo ! Nous en revenons à la remarque de Lebesgue : pour mesurer la longueur d'une pelote de ficelle, tu la pèses, et ensuite tu en coupes une longueur étalon, que tu pèses également. Le rapport des longueurs sera dans le rapport des poids...

De ce point de vue, les idées les plus simples auxquelles nous pouvons nous raccrocher, en [♲]𓂀 sont bien celles de "quantités conservées" et de "symétries", ce qui nous ramène à Noether. 

- D'accord, tu tiens ton point de départ [♲]𓂀, mais ensuite ?

- Le plus simple, a posteriori, me semble être de partir des groupes d'homologie. Considère un objet quelconque de dimensions n, concrètement en 4D pour un mouvement dans l'espace, ou en 3D dans un espace géométrique, pour fixer les idées. À cet objet, tu peux attacher un "volume" qui se "conserve" à travers toutes les transformations qu'il peut subir. Par exemple le vecteur vitesse en relativité (galiléenne v=const ou restreinte v.v̅=c²) ou un volume d'eau qui se conserve en le transvasant d'une flûte à champagne dans un bol de soupe.

Si tu définis ton objet par ses groupes d'homologie, ce volume est représenté par le dernier groupe, réduit à l'élément neutre e.

Autrement dit, cet "objet", que tu peux rattacher par une série de métaphores à l'objet final (*), identifié par {1} en [∃][⚤]𓁜, tu le vois également, avec tout le recul dont tu es capable, en [∃][⚤][#][♲]𓁜 comme l'élément neutre d'un groupe qui se définit en [∃][⚤]𓁜. Tout ceci est cohérent, puisque l'opération rattachée à la posture  [∃][⚤]𓁜 est la multiplication, dont {1} est l'élément neutre.

La fin de l'histoire étant connue d'avance, à savoir cette représentation finale d'un objet à n dimensions par son volume, autrement dit après n itérations d'un mouvement ↑ entre [⚤] et [#], que je note [⚤][#]ⁿ (ou ⁿ[#]), on commence par reconstruire l'objet en partant de la dimension 0D, à savoir les "points" de l'objet, pour passer ensuite aux arêtes entre les points en 1D, puis les surfaces en 2D etc.

Implicitement, je ne fais pas de différence entre le "point" vu comme élément d'un groupe, c.-à-d. dans une posture [∃][⚤]𓁜, et le "point" comme élément géométrique de dimension nulle, vu en [#]𓁜.

Ça mérite que l'on s'y arrête ! Dire que  j'ai une approche "topologique" de l'objet implique la possibilité de le voir dans une posture globale 𓁜, aussi bien que locale 𓁝 or, que pourrais-je voir d'un point dans cette posture 𓁝[#]? Rigoureusement rien : je reste dans un espace sans dimension, tourné vers l'objet initial 𓁝[#][∅] !

- Cependant tu restes cadré par [♲]𓁜, ce qui limite l'horizon du Sujet 𓁝[#][♲]𓁜[∅]𓂀.

- Oui, fort heureusement, c'est ce qui nous permet de parler rationnellement de ces choses. Mais cela revient à dire qu'il nous faut représenter notre "point" par un principe de "conservation" résultant de "symétries".

- Autrement dit, tu en reviens à la géométrie de Bachmann ? (note 3)

- Je pense qu'elle s'impose d'elle-même.

- Je te propose de le noter ici pour avancer dans cette mise en perspective générale, sinon tu ne vas pas y arriver.

- Soit, mais retiens au moins l'idée générale d'une définition "à rebrousse-poil" de tous les éléments de la géométrie, en partant du complexe pour arriver au plus simple : une droite est comme la pliure d'un plan, et un point se définit à partir de deux droites... Le point s'inscrit dans un espace 3D; et cette définition régressive, partant de là pour aboutir à 0D, me plait.

- Qu'est-ce que cela a de si original ?

- L'approche de Bachmann mène à toute une série d'équivalences entre "droites" et "points", qu'il est bien difficile de faire rentrer dans le carcan d'une approche immanente allant du simple au complexe, dans laquelle on irait du point élémentaire à la droite comme collection de points et de la droite à la surface comme collection de droites.

Ce manque d'ordre entre concepts est bien la marque d'une pensée au-delà de [⚤]𓁜, comme nous l'avions remarqué dernièrement.

- Sauf que les groupes d'homologie auxquels tu te raccroches se construisent à partir des points, "bordant" des arêtes, qui "bordent" à leur tour des surfaces etc...

- Tiens, oui, c'est vrai. Je me demande s'il n'y a pas là une belle rupture de symétrie à creuser ?

- Qu'as-tu en tête ?

- J'ai toujours cette petite musique quelque part dans ma tête, qui me serine en sourdine les paroles d'Alain Connes : l'espace physique a deux faces, l'une étant notre espace ordinaire (commutatif), qui se doublerait en chaque point d'un autre espace (non commutatif) où s'expriment les symétries attachées à ce point. N'avons-nous pas ici quelque chose du même genre ?

- Pose-lui la question !

- Dès que j'en ai l'occasion, c'est promis. Mais en attendant, cette réflexion en amène d'autres.

Acceptons l'idée que le  Sujet puisse raccorder notre "point" topologique, à l'élément d'un ensemble, dans un changement de posture élémentaire  [⚤]𓁝𓁜[#]⏩[⚤]𓁝𓁜[#], nous sommes de facto dans une approche locale de l'objet, c'est d'ailleurs à mon sens le propre d'une approche topologique : le regard tourné vers un objet final qui nous échappe absolument 𓁝[∅], je n'y reviens pas.

C'est parfaitement clair dans la définition du groupe fondamental d'un espace topologique. je t'en rappelle l'idée fondatrice : le Sujet se pose en un point "p" d'une surface qu'il ne sait pas appréhender. De là il explore la surface en traînant derrière lui une ficelle et revient à son point de départ, puis tire sur ladite ficelle. S'il ramène toute la ficelle à lui, la surface encerclée était "pleine", ou "continue", sinon, il  a tourné autour d'un "vide". Toute surface se résumant d'ailleurs au compte des "trous" qu'elle entoure. Avec cette idée que les trous sont en quelque sorte "orthogonaux" entre eux, de même que les chemins élémentaires qui te permettent d'en faire le tour. Je te laisse méditer à loisir sur cette magnifique image d'une chambre à air :

La place du Sujet est en p, et les deux chemins indépendants qu'il peut suivre sont a et b, et nous sommes dans la posture [⚤]𓁝𓁜[#]. La définition du groupe fondamental π_p=(1,a,b) quant à elle s'inscrivant en [⚤], après le retournement du Sujet [⚤]𓁝𓁜[#]⏩[⚤]𓁝𓁜[#] dont nous venons de parler

Si la construction des groupes d'homologie se construit également à partir de cycles faisant le tour de vides, le point de vue est différent. Reviens sur la présentation de Wildberger :

La figure au tableau est constituée de 3 points (x, y z) et de 4 arêtes (a, b, c, d). Maintenant, ce qui nous intéresse à ce stade du processus, c'est de repérer les "cycles" qui entourent des vides indépendants, ici les cycles générés par (a+b+c) et (c-d). Nous sommes donc, en accompagnant le regard que porte Wildberger sur la figure qu'il nous désigne au tableau, dans une position ex post.

Nous savons, sinon désigner les trous, tout du moins les cerner sans les parcourir, d'ailleurs l'algèbre que nous développons n'étant plus liée au parcours physique d'un chemin (i.e.: a+b+c=a+c+b), nous le confirme. Le Sujet est donc en [#]𓁜 dans la posture un peu paradoxale d'où il nous parle objectivement, le regard tourné vers l'objet final [∃][#]𓁜 d'un vide qui lui échappe absolument 𓁝[∅]𓂀. La seule conscience qu'il en ait se résume à la notation additive de l'opération de groupe, allant de paire avec le 0 comme élément neutre...

Je trouve extrêmement fort de considérer que l'introduction d'une face bordée par (c-d), à l'étape suivante, supprime un trou dans l'objet. Considérer que l'objet se constitue en remplissant un vide, ma semble d'une grande portée philosophique, et me rappelle immédiatement le problème de Monge cherchant le moyen optimum de transférer un tas de sable dans un trou (note 4) :

- Tu me donnes le tournis à toujours passer du coq à l'âne ! Et si tu te recentrais sur ton sujet ?

- Désolé... Il me semble donc que nous ayons une chaîne:

• (géométrie) qui partirait d'une conception des éléments de la géométrie comme de "quantités conservées" par des "symétries" en  [♲]𓁜, pour les constituer en [#]𓁜, dans un mouvement ↓: 𓁝[♲]𓁜⏩[#]𓁝𓁜[♲]⏩[#]𓁝𓁜;
• (topologie) La réflexion de Poincaré amène à caractériser des surfaces homotopes X vues localement d'un point p, par leur groupe fondamental π(X,p), dans un mouvement ↓ : [⚤]𓁝𓁜[#]⏩[⚤]𓁝𓁜[#];
• (groupes d'homologie) l'objet est vu ici en [#]𓁜 comme "déconstruisant" un vide étape par étape. 
  • La première est repérée en [⚤]𓁜 par une algèbre Zⁿ où n est le nombre de points élémentaires de la surface.
  • La dernière est repérée en [♲]𓁜 par un groupe d'homologie réduit à l'élément neutre.

Ce dernier mouvement est plus difficile à cerner, car il s'agit d'un processus itératif de construction de la suite des groupes d'homologie H_i, correspondant en fait à une diminution des degrés de liberté de l'objet, jusqu'à l'élément neutre final.

- Tu peux dire tout simplement que l'indice i de H augmente, et qu'à chaque étape, H_i est inclus dans H_i-1, où est le problème ?

- C'est vrai, mais on perd de vue que cette suite "mets en ordre" en [⚤] un objet de niveau [#] qui n'en n'a pas. Il y a comme de la diaphonie dans la représentation.

- Tu as tout simplement une rupture de symétrie en passant de [#] à [⚤].

- Oui sans doute faut-il que je m'y habitue ! Toujours est-il que nous avons ici un mouvement ↓, qui nous ramène à un comptage élémentaire (*)↑{1} en [∃][⚤]𓁜. Autrement dit : [#]𓁝𓁜⏩[⚤]𓁝𓁜[#]⏩[∃][⚤]𓁝𓁜[#].

En résumé, nous pouvons repérer les uns par rapports aux autres les trois mouvements associés respectivement à

• la géométrie (),
• le groupe fondamental () en topologie,
• les groupes d'homologie ().

  (1) (𓁝[♲]𓁜⏩[#]𓁝𓁜[♲]⏩([#]𓁝𓁜[♲]⏩(([⚤]𓁝𓁜[#]⏩[∃][⚤]𓁝𓁜[#]))))

J'ai noté () pour mémoire le passage de la topologie comme de la géométrie à l'algèbre, c.-à-d. le renversement [⚤]𓁝[#]⏩[⚤]𓁜[#].

- Belle scène pour le spectacle, mais quelle pièce y joue-t-on ?

Le 06/12/2020 :

- Ça fait pratiquement une semaine que je bloque sur cette question !

- Qu'est-ce qui te bloque ?

- C'est ce retour à Bachmann qui s'invite dans le discours. J'étais parti sur l'idée que la théorie des groupes d'homologie offre une vue globale, ex post [#]𓁜 de ce que la topologie aborde essentiellement ex ante, localement 𓁝[#], comme on le voit sur le schéma d'ensemble, toutes deux faisant le lien avec la théorie des groupes [⚤]𓁜, mais en voyant la scène finale, je me dis qu'en rester là serait louper l'essentiel, qui tient à l'approche de la géométrie par Bachmann, or, là nous partons à la dérive, bien loin de Galois...

- Que t'importe ? As-tu un train à prendre, une thèse à rédiger, un agenda chargé? Pose-toi sur le divan et dis-moi tout mon petit...

- Encore une fois, je vais parler de ce que je ne connais pas, mais en relisant l'article où j'y fais référence (note 3), deux ou trois choses me titillent l'esprit. Je recopie ici le passage pour en discuter plus à l'aise :

"...Or, Bachmann défini points et droites à partir de considérations portant sur les concepts de symétries et d'orthogonalité. (p. 151):

• La composée de deux symétries orthogonales est d'ordre 2 si et seulement si les axes sont orthogonaux

• La composée d'une symétrie orthogonale d'axe d et d'une symétrie centrale de centre A est d'ordre 2 si et seulement si le point A appartient à la droite d.

• La composée de 3 symétries orthogonales est une symétrie orthogonale si et seulement si les trois axes sont soit concourants, soit ont une perpendiculaire commune;
• La composée de 2 symétries centrales de centres distincts n'est jamais d'ordre 2.

À partir de là, Bachmann construit les axiomes communs à toutes les géométries:

J'ai recopié le texte d'Yves Martin, qui me semble très clair, pour en arriver à sa remarque:

"Dans une construction algébrique abstraite, les droites sont identifiées aux symétries orthogonales et les points à leur produit quand ce produit est d'ordre 2. On ne manquera pas d'être interpellé par le fait que ce haut degré d'abstraction dans la représentation de la géométrie est, d'une certaine façon, ce que nous enseignons aussi à l'école primaire quand nous expliquons aux enfants qu'une droite, c'est le pli obtenu par le pliage (le maître demande parfois de "repasser le pli obtenu au crayon noir"). Le point est alors obtenu par un nouveau pliage du pli sur lui-même: voici un exemple où les gestes les plus élémentaires de la géométrie contiennent en essence l'abstraction la plus aboutie de l'objet appréhendé."

Tu vois comme ce "point" qui me gênait aux entournures, se trouve ainsi propulsé aux niveaux les plus abstraits de notre Imaginaire !

- Et à quel niveau précisément ?

- A priori, le concept premier est celui d'orthogonalité, ce qui nous mène au minimum en IR. Le point serait donc "représentable" en IR, par un enchaînement de symétries orthogonales, mais le référé de cette représentation peut sans difficulté être rejeté jusqu'en I0, dans une approche résolument locale: I'm<IR<...<I0(=Im)."

Je m'étonne tout d'abord d'être autant en phase avec mes réflexions d'hier, avec peut-être cette précision : le concept d'orthogonalité trouve son importance en [#] (ou IR selon mon ancienne écriture) en rapport avec celui de symétrie en [♲] (ou I#).

- OK, mais qu'est-ce qui t'agite l'esprit ?

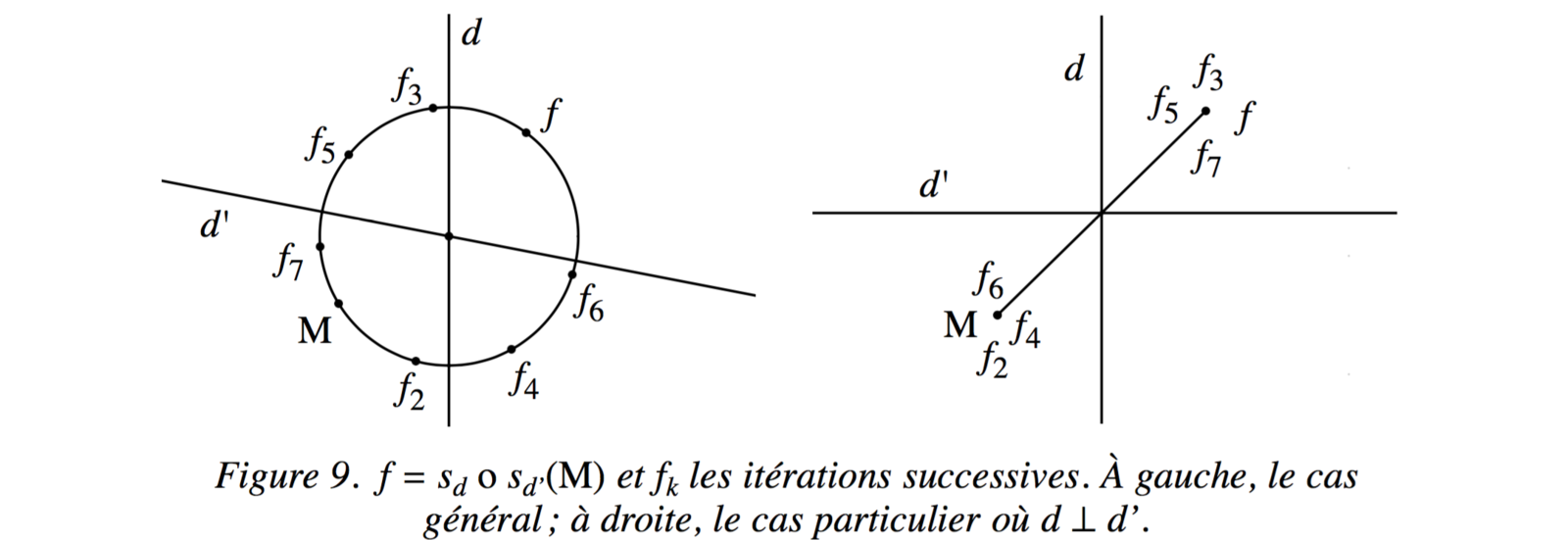
1/ L'enchaînement de deux symétries par rapport à deux droites reconduit un point M à sa place initiale lorsque celles-ci sont orthogonales et si tu restitues la scène dans le schéma général que nous venons d'établir, tu retrouves assez clairement le rapprochement que nous faisions entre le saut [#]↑[♲] et le triptyque d'Emmy Noether :

à partir d'une orthogonalité (en [#]), tu établies la stabilité en [♲] d'un élément (ici un point M qui revient toujours à sa place).

2/ Cette stabilité du point nécessite un va-et-vient, ou un mouvement. Ici, le mouvement est "synchronique", après mise en équivalence en [♲] d'une dualité ⊥ en [#] et répond au mouvement "diachronique" que l'on a discuté au niveau le plus élémentaire  [∃]⇅[⚤], avec (*)∈[∃]↑{1}∈[⚤] (i.e.: identité) suivi de {1}↓(*) (i.e.: propriété universelle).

Je vois donc dans l'axiomatique de Bachmann une résonance très profonde avec une voie qui commence à se dessiner assez clairement :

"l'orthogonalisation" des concepts en [#] est une sorte de "filtrage du Réel" qui nous permet d'organiser notre Imaginaire au niveau le plus haut en [♲].

- Je ne comprends pas trop ?

- Lorsque Descartes propose de repérer un point par ses coordonnées (x,y), il introduit une sorte de grille nous permettant de repérer le Réel...

- Il n'y a rien de très nouveau là-dedans...

- Oui, mais l'on s'aperçoit ici que le procédé est systématique, et à la réflexion, c'est à la base du concept "d'objet produit".

- Tu nous ressors ton Lawvere...

- Disons que j'en prends conscience comme d'une évidence à un niveau plus élevé, non pas en [⚤] où s'arrête Lawvere avec son topos logique, mais en [♲] où Bachmann se propose de reconstruire toute la géométrie, et je me dis que ce doit être là aussi qu'il sera possible un jour (si j'y arrive) de faire le lien, comme Grothendieck l'imaginait, entre le discret et le continu dans son topos à lui...

Par ailleurs, ce "filtrage" second en [#] peut maintenant être mis en perspective par rapport à l'organisation dichotomique caractéristique du niveau Imaginaire [⚤]. Prends-tu maintenant conscience de l'importance de cette révolution galoisienne qui a remis en lumière ce niveau [#], entraînant la faillite de toute pensée limitée à la dialectique ?

- Tu ne vas pas te faire que des amis, soit, mais quid de l'indétermination ?

- Ah ! c'est la bonne question ! N'oublie pas que l'indétermination caractérise la nécessité d'un saut diachronique or, ici en [♲], nous avons laminé toute différence de cet ordre, pour nous retrouver dans une description "à plat". C'est bien pour cela que l'on parle de "conservation". Lorsque tu enchaînes deux symétries, il s'agit d'un mouvement de pensée ne nécessitant aucun changement de posture du Sujet, qui reste en position ex post par rapport à chacune des deux droites (ou une droite et un point), pour repérer la position du point M, et de son reflet en f₁, puis le reflet du reflet en f₂ etc... La répétition devient plate : ⇆ ! (voir relecture au 30/12)

En écrivant ceci, je repense au retournement de fusée de Tintin entre Terre et Lune, passant d'un mouvement ⇅ à ⊥ pour parvenir à ⇆. Il serait intéressant de suivre ce schéma dans les méandres du cortex ! (note 5)

L'indétermination caractéristique des sauts vus ex post par le Sujet: [∃]⇅[⚤]𓁜 et [⚤]⇅[#]𓁜, n'est plus de mise dans un discours synchronique, fait de tautologies en [♲]𓁜 ! Ceci renforce mon intuition qu'il n'y a pas de conciliation entre mécanique quantique, avec les sauts diachroniques élément/ champ (i.e.: [⚤]⇅[#]), et la théorie de la relativité en [♲], sauf à prendre en compte les changements de posture du Sujet, comme nous le faisons ici...

- Tu rabâches mon ami, tu vieillis.

- Je ne rabâche pas, je digère, et je ne vieillis pas je mûris.

- Mouais, mais quoi de neuf là-dedans ?

- En parcourant à nouveau le livre d'Yves Martin, je retrouve cet encart résumant l'axiomatique de Bachmann :

Je note immédiatement cette forme γαγ^-1 associée à cette autre : α^γ qui me tire l'oeuil, comme l'importance de "l'ordre 2", en regard des sous-groupes alternés A_n, impairs.

- Bachmann ramène tout simplement la géométrie à la théorie des groupes, en [⚤]𓁜...

- Non, grave erreur de perspective ! Le concept d'orthogonalité n'aurait aucun sens à ce niveau ! Il s'agit bel et bien d'une montée Imaginaire, l'inverse de nos parenthèses () dans (1).

()^-1=[∃][⚤]𓁝𓁜[#]⏩[⚤]𓁝𓁜[#]⏩[#]𓁝𓁜[♲]⏩[#]𓁝𓁜[♲]⏩𓁝[♲]𓁜

Avec :

• Théorie des groupes : [∃][⚤]𓁝𓁜;
• Topologie algébrique : [⚤]𓁝𓁜[#]⏩[⚤]𓁝𓁜[#]
• Géométrie : 𓁝𓁜[#]⏩[#]𓁝𓁜[♲]⏩[#]𓁝𓁜[♲]
• Axiomatique de Bachmann : [#]𓁝𓁜[♲]⏩𓁝[♲]𓁜.

S'il faut y réfléchir, c'est bel et bien à ce niveau foncièrement relativiste [♲]𓂀 que l'on doit se tenir et ce n'est pas un hasard si Yves Martin aborde le sujet alors qu'il s'intéresse aux géométries non Euclidiennes (GNE).

- D'accord, tu as parcouru ton arbre Imaginaire [∃][⚤][#][♲][∅] dans les deux sens, mais qu'en retires-tu pour mieux comprendre Galois ?

- Je n'arrive pas à sentir l'évidence de ces actions conjuguées γαγ^-1 associées à la répétition du même α^γ, ni comment passer de là aux sous-groupes distingués.

- Je pense que tu pourrais déjà constater une similitude entre cette axiomatique développée en [♲] et la théorie des groupes en [⚤] : les deux s'écrivent "à plat", vues d'une posture ex post du Sujet : [⚤]𓁜 et [♲]𓁜.

- Oui, partons de là : des symétries en [♲] on passe aux orthogonalités en [#] et de ces dernières aux groupes en [⚤], il y donc deux expressions en parallèles de la notion de symétrie :

- Ta difficulté tient donc à ta propre incompréhension de l'étape (3), autrement dit du passage de la représentation géométrique des symétries à son expression algébrique. Ça ne nous avance pas beaucoup...

- Non, mais ça met les choses dans une perspective de niveau [♲].

Le 07/12/2020 :

- Peut-être est-il temps de revenir à cette différence identité/ idempotence qui te semblait si importante dans le passage de [⚤] à [#] ?

- Tentons le coup. Comment pourrait-on caractériser cette différence, si on tentait de l'exprimer en [⚤] ?

- Pour faire un parallèle avec la posture logique [∃][⚤]𓁜, il faudrait imaginer la posture 𓁝[⚤][#], qui ne semble pas très naturelle, puisqu'il s'agirait d'une régression de l'approche topologique au discontinu; or, par définition, cette position ex ante va de paire avec l'idée d'un objet initial ( ) impossible à cerner en [∅], ce qui est contradictoire avec la possibilité d'identifier les éléments d'un ensemble défini en [⚤] ...

- Qu'est-ce qui caractérise [⚤]𓁜 et disparaît dans la répétition des sauts [⚤]⇅[#]?

- La notion d'ordre, mon ami, la notion d'ordre ! Nous l'avons vu dernièrement en réfléchissant aux différentes définitions d'un espace topologique. (note 6)

- Soit, nous aurions alors :

• La position [⚤]𓁜 permet de la prise de conscience d'un ordre entre les éléments d'une succession, typiquement, l'ordre de succession dans N;
• La position 𓁝[⚤] serait celle d'une recherche d'ordre dans ce qui échappe au Sujet : à savoir les objets de niveau [#].

Nous aurions ainsi deux situations "symétriques" par rapport au niveau [⚤] :

• [∃][⚤]𓁜 : notre classique posture "rationnelle logique";
• 𓁝[⚤][#] : recherche d'un ordre entre les éléments de géométrie ou de topologie en [#].

Mais nous savons déjà que cette recherche est cadrée en [♲]𓁜 par un concept très général de "symétrie".

De ce point de vue très général, il semblerait que la théorie des groupes soit la réponse apportée par Galois, permettant le passage 𓁝[⚤]⏩[⚤]𓁜.

Ce passage serait alors caractérisé par l'élément neutre, e, vu tantôt comme représentant l'élément initial () pour l'addition, dans la posture 𓁝[⚤][∅], tantôt l'élément final (*) pour la multiplication, dans la posture [∃][⚤]𓁜.

- Ce qui serait cohérent avec l'idée d'élément neutre_♲ introduite au niveau [♲]𓁜?

- Oui, je pense effectivement que l'introduire à ce niveau [♲]𓁜 permettrait de le voir comme une "conciliation" ou symétrie_♲ des deux postures duales [∃]𓁜 et 𓁝[∅]; et ce lien entre symétries_♲/ théorie des groupes_⚤. Dans cette perspective, le dernier groupe d'homologie de l'objet, qui nous conduit à voir l'objet exister_♲ dans sa forme la plus achevée de volume_♲ ne peut que correspondre à l'élément neutre_♲ d'un groupe de symétries... 

L'élément neutre_♲ est le principe conservé d'une symétrie_♲ entre les éléments_⚤ {0}_⚤ et {1}_⚤ de l'objet discriminant {0;1}_⚤.

- Le point (2) de ton schéma ?

- Tout à fait, je pense que cela prend forme, petit à petit.

- Et pour en revenir au duo identité/ idempotence ?

- On est d'accord que le Sujet prend conscience de l'identité de l'objet final en [∃][⚤]𓁜 n'est-ce pas ?

- Tu le serines assez souvent, oui.

- Bien, nous en étions restés à (b) soit : 

1. Entre [∃]𓁜 et [⚤]𓁜, un saut ↑ est l'identification (*)↑{1}, et le saut inverse ↓ ne peut que tu conduire à l'objet final {1}↓(*) : c'est la propriété universelle de la théorie des catégories, et la répétition ⇅ n'amène aucune variation ;
2. En 𓁝[#]𓁜,
   1. l'enchaînement 𓁝↑𓁜⏩𓁝↓𓁜 conduit à I_A,
   2. l'enchaînement contraire 𓁝​​​​​↓𓁜⏩𓁝↑𓁜 conduit à e, autrement dit, tu passes d'un élément à l'autre d'une même section. L'enchaînement des opérations ⇅ conduit donc à explorer au hasard l'ensemble des éléments d'une section.

Tu remarqueras une parfaite similitude de mouvements entre les point 1 et 2.1, avec un "saut" ↑ suivi d'une régression ↓, qui ramène toujours à l'objet.

Par contre, démarrer par le mouvement inverse ↓ n'est pas envisageable dans la posture [∃][⚤]𓁜 puisqu'il faut commencer par identifier l'objet final pour en parler!

De ce point de vue : (y)

La régression de [#] à  [⚤] peut être vue en [♲]𓂀 comme une rupture de symétrie entre les séquences ↑↓ et ↓↑ au niveau [⚤]. 

- D'accord, mais qu'en est-il de 'l'objet" que l'on peut appréhender dans cette posture 𓁝[⚤][#]?

- À mon sens il ne peut s'agir que d'un "objet quotient".

- Attends un peu ! Tu es capable d'identifier chaque élément d'un tel objet.

- Pas vraiment, si le sous-groupe quotient est effectivement constitué d'éléments, chacun d'eux étant identifiable séparément des autres, tu n'a pas la possibilité de les distinguer à partir de ta position 𓁝[⚤][#] en ramenant un référé en [#] à un critère de niveau [⚤], dans un mouvement descendant ↓ ! L'idempotence est ici le concept central et répond à son symétrique parfait par rapport à [⚤] qui est l'identité. Le schéma de cette symétrie est: [∃]↑[⚤]𓁜 en regard de 𓁝[⚤]↓[#]...

- Ce n'est pas clair, à quoi correspond dans ce cas le mouvement d'identification 2.2 de ton tableau ?

- Vu de[♲]𓁜, les mouvements [∃]↑↓[⚤]𓁜 et [⚤]↑↓[#]𓁜, à savoir un saut suivi d'une régression sont similaires, tandis que la symétrie ↑↓ / ↓↑ correspond à un retournement du Sujet, autour de [⚤]: (voir c)

En résumé (en éludant le retournement implicite [⚤]𓁝𓁜[#]):

• ↑↓ <=> 𓁝[⚤][#]𓁜⏩𓁝[⚤][#]𓁜 <=> s.r=1_A identité d'un objet de niveau [#]
• ↓↑ <=> 𓁝[⚤][#]𓁜⏩𓁝[⚤][#]𓁜 <=> r.s=e idempotence

Présentation cohérente avec l'idée générale que tout objet de niveau [#] peut être défini en [⚤] comme "groupe quotient" : 1 point en  [#] est représentable en  [⚤] par l'ensemble Z, deux points par 2Z ou Z⊕Z etc...

- Il me semble que tu tournes en rond...

- J'ai simplement ramené toute la discussion au niveau [⚤] où s'expriment à la fois:

• la théorie des ensemble, tournée vers l'objet final, et
• la théorie des groupes qui tente de ramener de l'ordre en [#] à l'aide d'un concept de symétrie venu de [♲]. 

Il me semble qu'ainsi, nous pouvons plus facilement comprendre l'importance et la place qu'occupe le groupe quotient.

Du coup, la séparabilité entre "objets" au niveau [#] doit trouver sa traduction en [⚤].

- Attends un peu, je croyais que le saut [⚤]↑[#] nous faisait précisément passer du discret au continu ?

- Oui, dans une posture ex post [#]𓁜, mais qu'en est-il lorsque l'on régresse jusqu'en [⚤] où cette "continuité" n'a plus cours ?

- En ce sens, c'est peut-être la "séparabilité" implicite en  [⚤] qu'il s'agirait de caractériser en posture [#]𓁜, non ?

- La réponse s'impose d'elle-même : ce qui est "séparé" en [⚤] est "orthogonal" en  [#].

Je crois que nous y arrivons !

Le 17/12/2020 à 02h:

En relisant le passage sur Bachmann avant de m'endormir dessus, pour que ça décante tout doucement pendant mon sommeil, me vient cette idée: la répétition des sauts [#]⇅[♲] s'exprime en [♲]𓁜 en termes de symétries, tout simplement.

Nous avons donc cette évolution concernant l'automatisme de répétition si cher à Freud :

• [∃]⇅[⚤] : le concept de successeur ordonne les éléments en [⚤]
• [⚤]⇅[#] : orthogonalité entre concepts en [#]
• [#]⇅[♲]: les symétries en s'enchaînant forment des "objets" en [♲] 

Il faudrait en déduire la nature de l'objet à partir de là (x):

• [∃][⚤]𓁜 : l'objet est une "collection d'éléments";
• [⚤][#]𓁜 : l'objet se définit comme "produit";
• [#][♲]𓁜 : l'objet se définit par sa "conservation";
• 𓁝[⚤][#] : l'objet se définit comme "groupe quotient";
• 𓁝[#][♲] : l'objet se définit par ses "parties";

- Fais de beaux rêves là-dessus...

Le 17/12/2020 :

- Je n'arrête pas de penser à cette expérience faite sur des chats. L'un élevé depuis sa naissance dans un environnement ne comportant aucune ligne horizontale, l'autre dans un univers sans aucune ligne verticale. Et bien, une fois leurs cerveaux arrivés à maturité, le premier ne "voit pas" les lignes horizontales, ni le second les lignes verticales et ils se heurtent sans cesse à des grillages composés des éléments qu'ils n'ont pas intégrés.

- Où veux-tu en venir ?

- Au fait que nous n'apprenons pas en passant du simple au complexe, en passant par exemple du point à la droite. Penser, comme nous le faisons à la "droite des Réels", en nous questionnant sur la continuité entre points sur R est une question culturellement déterminée, assez récente au demeurant. L'animal que nous sommes n'apprend pas de cette façon.

- Tu remets en cause ton étagement Imaginaire ☯[∃][⚤][#][♲][∅]☯𓂀?

- Ce n'est qu'une représentation utile, qui me permet d'exprimer assez simplement la position qu'adopte un Sujet pour se repérer dans un monde qu'il définirait comme "sa réalité". C'est déjà un progrès par rapport à mon écriture initiale R<I0<I01<IR<I#<S, dans laquelle le signe "<" posait problème.

- Tu as cependant le signe ⏩ pour indiquer un changement de posture du Sujet, et donc une évolution temporelle, de l'ordre de la succession.

- Oui, mais il s'agit du temps narratif, qu'il me faut bien employer pour m'exprimer, autrement dit en position [∃][⚤]𓂀... Même si je parle du temps de la relativité pour un Sujet en position [∃][⚤][#][♲]𓁜𓂀.

- Il y aurait toujours un décalage entre la narration et l'objet du discours ?

- Oui, mais pas d'affolement : lorsque je dessine un portrait, j'exprime bien une esquisse en 2D d'un référé en 3D, ce qui ne nous empêche pas de nous comprendre. La difficulté concernant le temps est du même ordre.

J'aime à penser que ma représentation linéaire ☯[∃][⚤][#][#][♲][∅]☯𓂀 se boucle sur elle-même comme un ruban de Moebius où le "Réel" serait l'avers du "Symbolique" :

D'ailleurs, tu remarqueras sur cette photo que j'ai étiqueté le plus haut niveau de conscience rationnel, avant le vide en [∅], par cette représentation du ruban de Moebius [♲] marquant une analogie entre l'ensemble de l'Imaginaire et l'une de ses partie... De plus, je suis moi-même dans cette position [♲]𓂀 pour t'en parler. 

- Autrement dit, tu en reviens à une représentation fractale ? (note 7)

- Là encore, il ne s'agit que d'une esquisse. Le bouclage de l'Imaginaire sur lui-même, qui couperait le Sujet d'un environnement dont il procède à l'évidence, me conduirait à prolonger ma réflexion par une bouteille de Klein :

Le référé de cette image étant un objet en 4D.

- Ce qui nous conduit à un mouvement...

- Oui, je pense profondément que le Sujet ne peut se définir que comme mouvement...

- Tu nous ramènes au Yi King, au livre des mutations ?

- C'est plutôt rassurant de retomber sur ses pieds, non ?

- Nous voici bien loin de Galois ! Pourquoi cette méditation ce matin ?

- Je repensais à ce que j'ai écrit cette nuit :

• [∃]⇅[⚤]: le concept de successeur ordonne les éléments en [⚤]
• [⚤]⇅[#] : orthogonalité entre concepts en [#]
• [#]⇅[♲]: les symétries en s'enchaînant forment des "objets" en [♲] 

Le symbole ⇅ ne me semble pas adapté aux sauts [⚤]⇅[#] ou [#]⇅[♲], puisque la répétition ne se fait pas sur le mode de la succession, ce qui remet en cause l'idée originelle de Freud voyant l'Imaginaire comme un feuilleté répercutant le trauma du Réel jusqu'au niveau Symbolique.

- C'est toute ton approche que tu remets en cause !

- Philosopher, c'est parier, mais le cylindre de la roulette tourne toujours et il est encore temps de changer ma mise.

- Tu renies ton approche ?

- Je dis simplement qu'il faut élargir mon horizon. Certes, l'écriture  ☯[∃][⚤]𓁜𓂀 exprime clairement la position rationnelle logique élémentaire de Descartes, je n'y reviens pas.

Mais le "choc" du Réel peut nous frapper à tout niveau Imaginaire ! Lorsque la communauté scientifique a été bouleversée par la catastrophe ultraviolette, seuls quelques rares physiciens en ont été affectés. Tout le bouillonnement culturel qui en a résulté est passé inaperçu du reste de l'Humanité, bien que ce "choc" ait remis en cause toute la physique du XIX^è siècle [♲]𓁜⏩𓁝[♲], ce qui n'était pas une mince affaire !

Tu vois donc la difficulté qu'il y a à représenter le Réel ☯ à un seul bout de notre Imaginaire ☯[∃], quand il y a "trauma à tous les étages", si je puis dire.

- Si comme tu le penses le Sujet se définit par son mouvement, tu as malgré tout une trace historique du coup reçu, marqué précisément par ce changement de posture : [♲]𓁜⏩𓁝[♲].

- Admettons. Cependant, la conséquence du trauma est différente, selon le niveau où le choc est ressenti et de ça, Freud ne parle pas !

- Où veux-tu en venir ?

- Je pense à ma représentation des "sauts diachroniques" qu'il faudrait revoir.

- Que proposes-tu ?

- Si le sentiment de la répétition entre [∃] et [⚤] s'exprime bien ex post par [∃]⇅[⚤]𓁜, il faudrait changer de symbole pour exprimer les sauts entre [⚤] et [#], que l'on pourrait décrire ex post par [⚤]⊥[#]𓁜, quand le dernier saut entre [#] et [♲] se repère ex post par un principe de conservation, autrement dit une équivalence : [#]⇆[♲]𓁜, ce qui achèverait notre tableau.

- Et comment caractériserais-tu ces mêmes sauts vus en position ex ante ?

- Par les concepts à la disposition du Sujet dans cette position. Nous aurions donc l'ensemble de postures suivants :

• [∃]⇅[⚤]𓁜 & 𓁝[⚤]⇅[#]
• [⚤]⊥[#]𓁜 & 𓁝[#]⊥[♲]
• [#]⇆[♲]𓁜

- Quid de la dernière posture 𓁝[♲][∅] ?

- Elle marque la limite de la pensée rationnelle : le morphisme ayant l'objet initial comme domaine ou codomaine n'a pas de flèche, puisque le vide n'a pas d'élément.

- Je te sens soulagé ?

- Oui parce que j'ai enfin répondu à une question qui m'a été posée il y a déjà quelques années, et m'avait laissé coi. À l'époque, j'indicais et arrangeais ainsi les différents niveaux Imaginaires: I_k<I_k+1<I_k+2 etc. Et mon interlocuteur m'avait demandé à quel niveau je me situais, moi, pour introduire un tel ordre entre mes niveaux.

La réponse que je peux lui donner aujourd'hui est la suivante :

1. L'ordre est typiquement la prise en compte en [⚤]𓁜 de la répétition des sauts [∃]⇅[⚤]𓁜. Notion qui reste d'actualité dans le 1^er retournement [⚤]𓁝𓁜[#]⏩[⚤]𓁝𓁜[#], pour se perdre ensuite dans sa répétition (vue ex post) 𓁝[#]⏩[#]𓁜.
2. Dans le déroulé de ma narration, j'en reste à un enchaînement historique des différentes postures du Sujet, les signes ⏩ et ⇅ marquant un temps élémentaire de type [∃]⇅[⚤]𓁜, comme le pouls de Galilée.
3. Au delà de [⚤], il faudrait mieux se représenter les niveaux Imaginaires [#] et [♲] comme des poupées Russes enrobant ce coeur palpitant.
4. Le regard que je porte sur cette construction gigogne, hors discours, n'est plus rationnel et se rapporte à mon propre Imaginaire ☯𓂀☯...

Le 1^er point me permet de situer ma propre difficulté à comprendre quelque chose qui me pourrit la vie depuis ma première présentation au groupe CLE, à savoir une double interprétation de l'automatisme de répétition entre  [⚤] et [#] :

• Vu ex ante 𓁝_⇅[⚤][#] : je suis fondé à parler de répétition des sauts r.s ou r.s
• Vu ex post  [⚤][#]_⊥𓁜 : je caractérise la séparation des objets en [#] en termes d'orthogonalité.

Il y avait dans ma tête une sorte de diaphonie que je n'arrivais pas à cerner et bien c'est chose faite : je me parlais de deux points de vue à la fois !

Au fur et à mesure que je m'habitue à cette écriture hiéroglyphique, j'en précise les possibilités. L'idée d'utiliser les signes ⇅, ⊥ et ⇆ en indice de 𓁝 ou 𓁜 permettrait de condenser l'écriture. L'inconvénient est que ma pratique va demander un effort d'apprentissage au lecteur ! Avec cet avantage qu'elle permet une très grande précision, ce qui m'a permis de clarifier simplement un trouble qui me brouillait l'esprit depuis fort longtemps !

- Ça vaut le coup de faire le tour de la question, quitte à repiquer ultérieurement le passage dans un article de mise au point, non ?

- Soit. Après avoir caractérisé la position du Sujet ex post 𓁜 ou ex ante 𓁝 par rapport aux différents niveaux synchroniques ☯[∃][⚤][#][♲][∅]☯ structurant son Imaginaire, nous préciserons donc son regard à l'aide de ces indices.

Ce qui me permet d'apporter une ultime précision, quitte à être taxé de pinailleur :

• Les écritures [⚤]_⇅𓁜, [#]_⊥𓁜, [♲]_⇆𓁜 n'offrent pas de difficulté puisque le Sujet en position ex post a pleinement conscience des concepts en indice.
• De même, les positions 𓁝_⇅[#], 𓁝_⊥[♲] et 𓁝_⇆[∅] on également un sens, puisque le concept en indice reste acquis, après retournement du Sujet d'une position  _⇅𓁜 à 𓁝_⇅ ou d'une position_⊥𓁜  à 𓁝_⊥ et encore de  _⇆𓁜 à 𓁝_⇆.
• Par contre les positions  𓁝_⊥[#] ou 𓁝_⇆[♲] sont impossibles puisque le Sujet, ex ante par rapport au niveau synchronique considéré, n'a pas encore acquis le concept en indice.

- Mais tu nous as pourtant parlé de 𓁝_⇅[⚤] ?

- C'est lié au caractère même de l'automatisme de répétition au niveau [⚤]. Dès que tu itères le premier saut [∃][⚤]_⇅𓁜, autrement dit, après l'identification {1} de l'objet final (*) tu peux accepter cette écriture. En fait, toute l'algèbre comme la théorie des graphes est une écriture "à plat" en [⚤] et il n'y a pas cette différence locale/ globale, qui s'instaure dans l'approche topologique. L'idée de 𓁝_⇅[⚤] est une régression par rapport à cette approche topologique 𓁝_⇅[#]𓁜⏩𓁝_⇅[⚤]𓁜.

Par symétrie, je ne caractérise pas d'un indice particulier :

• La position finale [♲]𓁝[∅] pour les raisons que nous avons déjà vues : l'objet initial n'a pas d'élément;
• La position initiale [∃]𓁜[⚤] : c'est l'axiome d'existence ramenant tout au Sujet lui-même, comme Descartes nous l'a appris. 

En résumé, nous avons donc les postures rationnelles suivantes (en rappelant que toute posture 𓁝 rationnelle est subordonnée à une prise de conscience ex post 𓁜).

• ☯[∃]𓁜
• [⚤]_⇅𓁜 et 𓁝_⇅[⚤]𓁜 (Le rouge indique la position active)
• [#]_⊥𓁜 et 𓁝_⇅[#]𓁜
• [♲]_⇆𓁜 et 𓁝_⊥[♲]𓁜

En complément, nous avons une limite de rationalité propre à chaque niveau nécessitant d'accepter certains axiomes adéquats, pour passer de 𓁝 à 𓁜 :

1. (𓁝_⇅[⚤]𓂀 position récessive après le stade du miroir  [⚤]𓁝|𓁜[#])(voir 3)(d)
2. 𓁝_⇅[#]𓂀
3. 𓁝_⊥[♲]𓂀
4. (𓁝_⇆[∅]☯𓂀 position non "fermée" par une posture [∅]𓁜 marquant la limite ultime de toute rationalité).

Tu vois que ce n'est pas si compliqué, finalement.

- OK, mais pour en revenir à tes chats ?

- Nos concepts géométriques s'imposent à l'esprit de l'enfant après que ses yeux ont permis à son cortex de former leurs représentations, bien avant l'apprentissage du langage, dans un processus qui a décanté des millions d'années au sein du vivant, avant que Descartes nous explique comment bien penser. Autrement dit, nous sommes familiers des courbes et des surfaces bien avant d'y voir des ensembles de points, ce qui donne une grande consistance à l'approche de Bachmann : pour expliquer une droite à un enfant, on lui demande d'imaginer la pliure d'une feuille, et pour imaginer un point, on lui demande de replier une seconde fois cette pliure.

- Et l'apprentissage est transcendant, il lui vient du maître...

- Tout juste, rien n'a changé depuis Socrate (voir "Le Menon").

- Bon, soit, mais tu nous entraînes bien loin de l'objet de cet article.

- Pas tant que cela. Reviens à nos enchaînements sections/ rétractions.

• En position ex ante, on parle bien d'une succession s.r ou r.s, dans la position 𓁝_⇅[⚤][#] et l'objet quotient se constitue bien à partir d'une telle succession, de la même façon que l'objet se définit comme un ensemble de points qu'il est possible d'ordonner en [⚤]_⇅𓁜, tout ceci reste cohérent.
• Par contre, l'objet quotient est vu comme "séparé" du groupe dans lequel il se définit par une orthogonalité qui n'a de sens que d'un point de vue géométrique ou topologique [⚤][#]_⊥𓁜.

Et toute ma réflexion dans cet article concerne bel et bien le passage de cette orthogonalité en [#]_⊥𓁜 à son expression algébrique en [⚤]_⇅𓁜.

- Je suppose que c'est en rapport avec cette anamorphose qui traîne sur cet article depuis le 06/12 ?

  - Oui, j'aime bien l'idée de ce plongement en 3D grâce auquel l'objet prend sens (ici un oeil), à partir d'une base aussi plate qu'illisible. Je pense à notre problème de cette façon : 

• La succession des sections/ rétractions, en position 𓁝_⇅[⚤][#] permettrait de parcourir cet objet représentable en [#]_⊥𓁜;
• Il nous reste à comprendre comment isoler cette trace à plat en [⚤]_⇅𓁜 sur le plan sans pouvoir lui attacher une signification perdue dans la dégénérescence [#]_⊥𓁜⏩[⚤]_⇅𓁜.

- Tu indiques une rupture que l'on ne retrouve pas dans l'anamorphose, puisque l'on passe de la représentation plate à son élévation par déformation continue, sans incertitude.

- C'est tout le problème, que l'on a bien cerné je le pense, tout d'abord dans notre tableau (3), ensuite dans la liste (d)...

Le 19/12/2020 :

- J'ai passé la journée d'hier à corriger ce que j'avais écrit le 17, avec l'introduction des indices pour préciser le concept diachronique utilisé par le Sujet, tout content de cette facilité d'écriture, et ce matin (enfin, quand je dis ce matin...) en relisant les axiomes de Bachmann, je ne peux m'empêcher de vouloir y rapporter mes éléments de construction...

- Tu fais de la géométrie maintenant ?

- Pas moi, mon cerveau. J'ai une intelligence essentiellement visuelle, et je ne considère avoir compris quelque chose qu'en le visualisant; mon utilisation de glyphes est assez significative à cet égard. D'ailleurs l'abandon d'une écriture amenant à des expressions littérales telle que I_k<I_k+1, m'a libéré des connotations mathématiques qu'elle véhiculait, ce qui me conforte dans cette voie.

Bref, il ne t'a pas échappé que cette axiomatique reste quelque peu ambigüe puisque l'on y parle de "symétrie par rapport à un point", avant de définir le point par des symétries, et de "symétrie par rapport à une droite", avec de définir la droite par des symétries.

- Tient, oui, c'est vrai, et donc tu abandonnes cette approche ?

- Au contraire : j'en suis ravi ! C'est le signe que nous sommes effectivement à un niveau Imaginaire où l'ordre, comme le temps n'ont plus cours ! Autrement dit en [♲]. De plus, et paradoxalement, compte tenu de cet univers immobile, les définitions sont basées sur des mouvements...

- Tu penses au moteur immobile d'Aristote, ou à la "causa sui" de Spinoza ?

- Plus modestement à l'idée de "conservation du mouvement" caractéristique de la relativité, qu'elle soit de Galilée ou d'Einstein. Et donc, comme tu le vois, tout ceci est cohérent.

Mais je m'égare.. Pour en revenir à Bachmann, donc, il part de deux éléments indéterminés, à partir desquels il construit ses mouvements élémentaires, c.-à-d. les symétries par rapport à un point et à une droite...

- Et ?

- Nous aussi nous partons de deux mouvements élémentaires :

• Une "rotation" du Sujet sur lui-même 𓁝|𓁜, initiée chez l'enfant au stade du miroir,
• Un "saut" diachronique, qu'il soit ⇅, ⊥ ou ⇆.

Par ailleurs, c'est d'instinct pourrait-on dire, que j'ai introduit la posture 𓁝_⇅[⚤]𓂀 comme symétrique d'une posture topologique [#]_⊥𓁜𓂀 qui la précède dans le développement historique des mathématiques. Autrement dit, par un soucis de symétrie relevant du niveau [♲]_⇆𓁜𓂀 de mon propre Imaginaire. 

Si tu y réfléchis bien, tout ce que j'écris ici, dans cet article, procède d'un soucis de symétrie de mes représentations qui est purement d'un niveau [♲]_⇆𓁜 où je situe également l'axiomatique de Bachmann... Il est donc raisonnable de boucler sur lui mon approche...

Il me reste donc à préciser la syntaxe de mon écriture hiéroglyphique par analogie avec cette axiomatique pour voir ce qu'il en ressort. Inutile de préciser que les réflexions qui suivent sont de niveau [♲]𓁜...

- C'est-à-dire ?

- Le propos est délicat, puisque je vais faire des rapprochements en [♲] entre des niveaux [⚤] et [#], qui précisément ne sont pas réductibles l'un à l'autre.

- Une dernière chose avant de commencer ton exploration : parlons-nous de l'objet ou du Sujet ?

- L'Imaginiare d'un Sujet lui permet d'appréhender les objets et de se situer par rapport à eux. Nous discutons ici de la structure même de cet Imaginaire, c'est dire que le Sujet est l'objet de mon discours. Notre objectif est de rapprocher la façon qu'a un Sujet quelconque 𓁜 de se représenter les objets et ma façon à moi, Sujet particulier et auteur du ce discours 𓂀, de rapprocher en [♲]𓁜𓂀 la structure Imaginaire du Sujet de celle de ses représentations.

- Ça donne une représentation fractale...

- C'est nécessaire pour que la démarche soit ouverte et donc consistante.

- OK, passons à cette syntaxe.

- Revenons à cette scène Imaginaire où s'agite notre Sujet, en utilisant cette fois notre notation indicielle pour préciser les concepts diachroniques à disposition du Sujet dans chacune des positions qui peut, potentiellement, occuper : ⇅⊥ ⇆ .

(nota: pour alléger l'écriture, je représente une rotation du Sujet 𓁝_⇅|_⇅𓁜 par 𓁝_⇅𓁜).

☯[∃]𓁜|𓁝_⇅[⚤]𓁝_⇅𓁜[#]𓁝_⊥𓁜[♲]𓁝_⇆𓁜[∅]☯_⇆𓂀

J'avoue que les positions extrêmes  sont toujours les plus délicates, parce qu'à la limite de la rationalité, quitte à revenir sur ce que j'ai pu en dire précédemment.

- De quoi parles-tu ?

- Des positions [∃]𓁜|𓁝_⇅[⚤] et [♲]𓁝_⇆𓁜[∅]. 

Je ne peux pas écrire [∃]𓁝|𓁜[⚤] parce qu'à ce stade élémentaire, le Sujet n'a pas l'expérience du miroir, et donc pas conscience de lui-même en tant que Sujet. C'est moi 𓂀 qui par abus de langage le vois comme "Sujet" [∃]𓁜𓂀 de même que la mère parle de son bébé comme d'un Sujet, et l'appelle par un nom qui n'a pas de sens pour lui. Par ailleurs, comme nous l'avons vu, la position 𓁝_⇅[⚤] n'apparaît que tardivement, comme dégénérescence d'une position plus élevée.

À l'autre extrémité de l'Imaginaire, j'écris 𓁝_⇆[∅] en partant du principe qu'il s'agit d'un retournement à partir de _⇆𓁜, autrement dit dans un processus immanent. Mais dans la construction du Sujet, le Symbolique s'impose à lui sans se préoccuper originellement de se justifier 𓁝☯𓂀. La construction 𓁝_⇆[∅]☯𓂀 reste très tardive et pour tout dire, relève du domaine de la philosophie...

- De la tienne à l'évidence.

- Comment pourrait-il en être autrement ? Ceci dit, le reste est assez mécanique, et c'est par là qu'il faut attaquer : 

([⚤]𓁝_⇅𓁜[#]𓁝_⊥𓁜[♲]_⇆𓁜)_⇆𓂀

Accroche-toi, ça va secouer !

Dans le discours ( ) porté par 𓂀, en [♲]_⇆𓂀 très précisément, nous avons trois entités irréductibles l'une à l'autre [⚤], [#], et [♲] que je 𓂀 pourrais dire "orthogonales" entre elles à un niveau descriptif [#]⊥𓂀. Ça nous donnerait ceci :

• "niveaux synchroniques" [⚤], [#], [♲] ⇆ "axe de symétrie de Bachmann".
• "pivotement du Sujet sur lui-même" 𓁝|𓁜 ⇆ "symétrie par rapport à un point", le Sujet étant ce "point" lui-même.

 Pour avancer, je dois compléter mon écriture avec les notations génériques suivantes (dans laquelle les différents niveaux [⚤], [#], [♲]  seront traités de façon équivalente) :

• Un pivotement du Sujet sur lui-même 𓁝|𓁜 (où | équivaut au point de Bachmann)
• Un pivotement du Sujet autour d'un niveau synchronique 𓁝[α]𓁜 (où [α] équivaut à l'axe de symétrie α de Bachmann)

- Voilà une énième variante de ton écriture...

- Oui, j'avoue que tout ceci est encore en gestation...

- Pourquoi ne pas représenter la rotation du Sujet autour de lui-même par un simple point 𓁝.𓁜 et autour d'un niveau synchronique par un axe 𓁝|𓁜? Tu retrouverais ainsi les symétries par rapport à un point ou un axe de Bachmann?

- J'ai hésité, mais l'on risque de ne pas bien voir le point, et puis, j'ai toujours en tête les bra/ket de Dirac, auxquels je me réserve de revenir :

• 𓁝|𓁜         <=>      ⟨𓁝|𓁜⟩
• 𓁝[α]𓁜     <=>     ⟨𓁝|α|𓁜⟩

L'analogie me semble assez frappante pour vouloir en conserver la trace, mais avançons.

Les objets sur lesquels nous appliquons nos mouvements Imaginaires étant des "objets du discours" sont, selon leur origine : 

• des "percepts" avec l'objet final (*) en perspective [∃]𓁜;
• des "concepts" avec l'objet initial ( ) en perspective 𓁝[∅].

L'idée de JJ Changeux selon laquelle une "prise de conscience" d'un objet est le rapprochement Imaginaire entre un concept et un percept (le concept étant acquis par avance, bien entendu), implique que :

toute "prise de conscience" du Sujet est un retournement, soit autour de lui-même 𓁝|𓁜, soit autour d'un niveau synchronique 𓁝[α]𓁜.

C'est une généralisation du retournement primitif de l'enfant 𓁝_⇅𓁜⏩𓁝_⇅𓁜 se tournant vers sa mère pour lui montrer son image dans la glace, cette dernière lui confirmant que cette image le représente 𓁝_⇅[#]𓁜⏩𓁝[#]_⊥𓁜, et donc qu'il n'est pas elle (passage de la répétition du même ⇅ à la différence ⊥).

Corollaire :

Le Sujet est conscient tant qu'il enchaîne des rotations de type 𓁝|𓁜 et 𓁝[α]𓁜

Hypothèses :

Le Sujet est "incident" ou "colle" à un niveau [α]𓁜, dans la position ex post (i.e.: le concept diachronique utilisé par 𓁜 est du niveau synchronique incident)

• [⚤]_⇅𓁜 ;
• [#]_⊥𓁜 ;
• [♲]_⇆𓁜.

À partir d'une telle position, un "saut diachronique" [α]𓁜⏩[α]𓁜 est "conscient" s'il est décomposable en produit de 𓁝|𓁜 et de 𓁝[α]𓁜.

1/ Une montée diachronique ou "saut" est le produit d'une symétrie de type 𓁝|𓁜 et d'une symétrie de type 𓁝[α]𓁜 (i.e. : 𓁝|𓁜x𓁝[α]𓁜)

2/ Une descente diachronique ou "régression" est le produit d'une symétrie de type 𓁝[α]𓁜 et d'une symétrie de type 𓁝|𓁜 (i.e. : 𓁝[α]𓁜x𓁝|𓁜)

Notre produit est donc antisymétrique, mais nous retrouvons bien l'idée géométrique qu'un point est incident à deux droites (i.e.: [α]𓁝|𓁜[α]) et qu'une droite est incidente à deux points (i.e.: 𓁝[α]𓁜).

En manière d'exercice, voyons l'effet du produit 𓁝|𓁜x𓁝[α]𓁜 sur quelques concepts usuels.

• (dichotomie_⚤𓁝⇅𓁜x𓁝[#]𓁜 ⇆orthogonalité_#)𓂀

Pour alléger l'écriture, on peut faire l'ellipse du Sujet en remarquant qu'il part d'une position ex post, pour arriver à une autre position ex post :

• (a) : (dichotomie_⚤⇅[#] ⇆orthogonalité_#)𓂀

Tu vérifies ici l'antisymétrique déjà repérée : l'opération 𓁝⇅𓁜x𓁝[#]𓁜 (ou ⇅[#]) n'est pas commutative car dichotomie_⚤[#]⇅ ne voudrait rien dire...

Continuons par:

• (b) : (orthogonalité_#⊥[♲]⇆conservation_{♲​​​​​​​})𓂀
• (c)=(a)(b) : (dichotomie_⚤[#][♲] ⇆conservation_{♲​​​​​​​})𓂀

L'équivalence (c)=(a)(b) exprime le passage du Sujet de [⚤] à [♲] comme le produit de deux sauts diachroniques élémentaires  de [⚤]𓁜 à [#]𓁜 et de [#]𓁜 à  [♲]𓁜. 

L'analogie entre la structure Imaginaire et l'axiomatique de Bachmann semble se limiter à ce type de produit. (note 14)

Le 20/12/2020 :

- Ça m'énerve toute cette histoire ! Nous sommes le 20/12 et je voulais boucler cette année sur une parfaite compréhension de Galois, après un détour par la physique, pour revenir l'esprit serein sur une réécriture de l'ensemble de mon approche à l'aide des topos et de la théorie des catégories en 21; en gros, reprendre mon 1^er exposé au CLE (note 8) après une lecture plume en main de Mc Lane. Mais je ne vais pas réussir à tenir cet agenda si je reste bloqué.

- Tu paniques, Arrête ! Passe en mode d'associations libres. Qu'as-tu en tête lorsque tu vois cette anamorphose ?

- J'avais l'intuition que le bord du miroir, au contact du plan est comme la base d'un espace vectoriel.

- Mais ici il n'en est pas question...

- Par analogie, je me représente ce "sous-groupe distingué" comme le bord du groupe qu'il délimiterait, au sens que le concept de "bord" a lorsque l'on parle des groupes d'homologie. Et puis il y a cet "aller-retour"  dans la définition qui m'obsède :

"soit G un groupe, et H un sous groupe de G, ce dernier est distingué si (∀y∈G I y^-1Hy∈H)"

- Eh bien, commence déjà par travailler là-dessus. Pourquoi cette obsession ?

- Parce qu'on retrouve cette forme partout.

- Vas-y, déroule...

- Sa forme la plus primitive est sans doute dans la "reconnaissance des choses" :

• Tu identifies l'objet final (*)_∃↑{1}_⚤
• Tu vois en l'objet final ce que tu as identifié {1}_⚤↓(*)_∃

- Je ne comprends pas trop bien ?

- Tu ne vois plus de l'objet offert par ton environnement que ce que tu as pu identifier. Pour ainsi dire tu fais exister ton rêve, c'est ça l'essence de la propriété universelle {1}_⚤↓(*)_∃ : tu habilles l'existence, hors de toi, venue du Réel, des oripeaux de ton Imaginaire. C'est la prise de conscience vue comme la rencontre entre un percept et un concept selon JP Changeux.

À l'autre bout de l'Imaginaire, il y a cette idée que l'objet se révèle par ses symétries, même si je ne peux pas m'en saisir. C'est assez simple à comprendre note bien : l'objet est repérable si lorsque je tourne autour il reste inchangé, il peux même être vide à la limite. Il y a bien l'idée de s'en éloigner pour y revenir. C'est implicite dans la définition du groupe fondamental de Poincaré π(X,p), et nous le retrouvons dans l'axiomatique de Bachmann...

- Stop ! Arrêt sur image. Il faut développer le rapprochement que tu fais entre Poincaré et Bachmann.

- Ils ne sont pas au même niveau Imaginaire. 

Poincaré parle d'homotopie, ce qui suppose une déformation continue dans le temps, avec un temps ⊥ à l'espace, c'est visible lorsque tu fais des diagrammes de déformation d'un objet. Nous sommes donc en [#]_⊥𓁜. Mais le groupe fondamental, à partir d'un point p sur une surface X, est une approche locale, et donc vue de 𓁝_⇅[#], ce qui permet le passage à une expression algébrique, après retournement du Sujet : 𓁝_⇅[#]⏩[⚤]_⇅𓁜.

Bachmann, quant à lui est pleinement en [♲]_⇆𓁜. Il ne s'agit plus de "tirer une ficelle derrière soi" dans une action temporelle 𓁝_⇅, mais d'un exercice "à plat" du Sujet _⇆𓁜, consistant à combiner des symétries. Là où Poincaré définit localement en p un groupe fondamental π(X,p), Bachmann définit globalement un ensemble Δ de "générateurs d'ordre 2" permettant d'engendrer des "objets".

Par sa position Imaginaire, Δ_♲ est donc plus élémentaire, plus fondamental que π(X,p)_# or les éléments de  Δ_♲ sont d'ordre 2, et nous retrouvons ici, mais dans un mouvement synchronique ⇆, le mouvement diachronique élémentaire ⇅ identification/propriété universelle.

Comme tu le vois, j'ai bien aux deux bouts de ma chaîne en [∃] et [♲] ce besoin d'un "aller-retour" du Sujet à l'objet.

- Et tu restes toujours coincé au milieu...

- Oui. 

- Je crois qu'il te faut prendre le temps nécessaire pour bien comprendre la nature même de ces axiomes de Bachmann avant de continuer. 

- Il y a une ambiguïté dans la définition de Δ, c'est un "ensemble" d'éléments, certes, mais ces éléments sont des isométries dont seuls les produits d'ordre 2 ont un sens géométrique. Dès lors, quel est la différence avec le groupe Γ ?

- Pour le dire simplement ces éléments sont des symétries orthogonales, à partir desquelles sont construites les "droites" et les "points" de la géométrie. Le terme de "droite" renvoyant à la géométrie Euclidienne pour aider à la représentation. Le concept d' (orthogonalité)_# (ou ⊥_#) s'exprime ici par (être d'ordre 2)_♲, (ou (aIb)_♲) c'est-à-dire par un retour à l'origine après "un tour complet" ⇆ "un aller-retour". C'est la signification de aIb: (ab)²=1.

Autrement dit le concept (aIb)_♲⇆𓁜 se représente géométriquement par des itérations 𓁝_⇅(⊥)_# et s'écrit algébriquement par ((ab)²=1)_⚤⇅𓁜. 

Le mouvement
(⊥)_#𓁝_⊥𓁜⏩𓁝_⊥𓁜[♲]⏩(aIb)_♲⇆𓁜, avec le saut 𓁝_⊥[♲]⏩[♲]_⇆𓁜 
doit en principe se caractériser par la conservation d'une quantité, il s'agit en l'occurrence des "droites" et "points" géométriques vus comme "produits" d'isométries. CQFD.

- Tu bétonnes devant ta cage, mais il n'y a personne en attaque !

- Désolé, je n'ai plus mes jambes de vingt ans; laisse-moi le temps de souffler.

Pour en revenir à ta question, il me semble (ça reste à vérifier) que Δ soit un sous-groupe de Γ (éléments α, β, γ...), dont les éléments (a, b, c...) permettent de produire des "objets" (P, Q...) représentables géométriquement, tels que "droites" et "points" en géométrie Euclidienne.

- OK, mais quid des axiomes d'incidence pour commencer ?

- J'avoue que l'axiome 1 semble un peu tordu de prime abord. Sans doute à cause de l'ambivalence du concept de droite, vu primitivement comme "axe de symétrie", à partir de quoi tu définis le point P comme produit de deux symétries ab², pour revenir ensuite à la droite, comme axe de symétrie incident à 2 points P et Q....

- Il s'agit d'un axiome, et puis ça permet de s'émanciper de la géométrie Euclidienne: si ton axe de symétrie se tord, la droite résultante se déforme en conséquence.

- Oui, oui, j'entends bien, mais tu vois à quel niveau d'abstraction nous atteignons! Cette circularité en particulier interdit totalement d'y voir un prédicat de niveau (logique)_⚤ !

Une fois la pilule avalée, le second axiome glisse plus facilement.

- Continue, tu me sembles bien parti, quid des axiomes des 3 symétries ?

- Le passage de 2 à 3 est toujours intéressant. C'est omniprésent en maths avec l'associativité : (a,b),c=a,(b,c)=(a,b,c) que tu retrouves un peu partout, ou encore dans la relation de Charles : IACI≤IABI+IBCI.

J'avoue avoir du mal à visualiser l'axiome 3. Néanmoins, ça me rappelle un passage de NJ Wildberger concernant le groupe de symétrie associé au cube (l'un des 5 solides de Platon):

Si tu te places sur un sommet pour faire 3 rotations, ceci revient à effectuer une symétrie par rapport à la diagonale d du cube passant par ce sommet. Je pense que c'est ce que nous retrouvons ici...

Pour l'axiome 4, l'axe g est la perpendiculaire commune à a, b et c. Si tu éclates ton cube précédent, je pense qu'il y a moyen d'imaginer que la diagonale d se déplace également... Il faudrait faire des projections pour s'en convaincre...

- Je sens que tu fatigues, mais que diras-tu de l'axiome d'existence du plan ?

- Il me semble que les droites j sont toutes celles d'un plan défini par les axes concourrents a⊥b. Mais c'est plus restrictif que le plan projectif, puisque privé du point origine ET des deux droites a et b...

- Mouais, tu me sembles encore peu assuré dans ton exploration. Es-tu assez solide pour attaquer le morceau de bravoure ?

"Le groupe Γ agit naturellement par conjugaison sur lui-même et donc en particulier sur Δ. L'action d'un élément γ de Γ sur un autre élément α donne pour résultat γαγ^-1 et se notera α^γ. On remarquera que si aIb alors a^b=a et b^a=b. De même si PIa alors P^a=P et a^P=a, ce qui donne tous les invariants par une symétrie orthogonale."

- J'aurais bien besoin d'être guidé. J'ai cherché sur le web sans rien trouver de bien consistant... Deux choses me perturbent :

1. L'évidence de cette "action par conjugaison" m'échappe. D'où Bachmann la tire-t-il ?
2. L'écriture α^γ me renvoie directement à la théorie des catégories, mais s'agit-il de la même idée ?

- Pour répondre au point 2/ Frederich Bachmann a fait ses études dans les années 1927 et a produit son axiomatique en 1959, il est peu probable que sa notation ait quelque chose à voir avec la théorie des catégories ! N'est-ce pas plutôt lié à l'idée de rotation et à l'écriture des nombres complexes, plus en vogue à l'époque ?

L'écriture rappelle celle d'une rotation sur le cercle unité du plan complexe. Le symétrique d'un point z=e^iφ par rapport à une droite passant par l'origine et d'angle θ/2 est z= e^i(θ+φ). L'opération inverse te ramène à z=e^iφ, et si θ est une fraction de 2π, telle que θ=2π/γ, alors z^γ=z^i(2π+φ)=z^iφ.

- Effectivement, ça paraît plus évident à la réflexion. Mais alors, tu remarqueras que cette écriture α^γ au niveau [♲] (ou α^γ_♲) est beaucoup plus pauvre que la rotation e^iθ dans C (ou e^iθ_#) au niveau [#]. Nous n'avons plus ici que l'action γ et sa réciproque γ^-1 pour agir sur α !

- Ça ressemble plutôt à un spin, non ?

- Pour les éléments dans Δ, oui, à rapprocher de la notion d'"observable", voire la prise de conscience du Sujet par lui-même 𓁝I𓁜 ... (note 9)

Mais pour en revenir au cas général, en Γ, il semble bien que nous ayons là le principe fondamental de niveau [♲] conduisant à cette définition des sous-groupes distingués en [⚤]...

- Tu radotes. Tu as commencé l'article là-dessus.

- Désolé, mais l'idée ne m'est pas encore familière, et je ne dois pas être le seul dans ce cas, car Bachmann est pratiquement ignoré en France... Lamentable !

- D'accord, mais as-tu avancé dans la régression de [#] à [⚤] ?

- Ce qui est certain, c'est qu'appliqué à un point M, l'enchaînement des actions γαγ^-1 ne ramènera pas M à sa place originelle, sauf cas particulier, pour les symétries de Δ.

Il faudra y revenir...

Le 22/12/2020 :

- Je ne suis qu'une vieille bête au cerveau rabougri.

- J'espère que ce n'est pas moi, ton reflet, qui t'emmènes à cette prise de conscience au moins ? Dis-moi tout.

- J'ai beaucoup de mal à comprendre à quoi correspond cette action en retour γαγ^-1, mais je perds de vue que α lui-même est une action. C'est vrai en [♲]𓁜 où α est une symétrie, mais ce l'est également en [⚤] ou nous parlons de groupes de symétries.

- Tu le découvres maintenant ?

- Non; je le "savais", sans en prendre pleinement la mesure, comme un enfant récite la table des multiplications ou un curé son bréviaire. Mon esprit est littéralement pollué par cette habitude que nous avons de "voir" les objets de notre entourage. J'ai beau le savoir, j'ai du mal à élever mon propre esprit au-delà de (☯[∃][⚤])_⇅𓂀 !

- Dans ce cas, comment peux-tu nous parler des postures du Sujet jusqu'en  (☯[∃][⚤][#][♲]​​​​​​​𓁜)𓂀?

- C'est une question de maturité. Je me sers de béquilles cartésiennes pour approcher ce qui m'échappe, d'où ces allers-retour, cet automatisme de répétition qui marque bien le niveau où je me débat. Au lieu d'avoir (☯[∃][⚤][#][♲]​​​​​​​𓁜)_♲⇆𓂀, ma propre position est plutôt de cet ordre : (☯[∃][⚤][#][♲]​​​​​​​𓁜)_⚤⇅𓂀... Autrement dit, je n'arrive pas au niveau de "compréhension" des concepts que je tente de présenter.

- Soit, et alors, en quoi consiste cette prise de conscience matinale ?

- J'en suis toujours à  ces groupes distingués :

"soit G un groupe, et H un sous groupe de G, ce dernier est distingué si (∀y∈G I y^-1Hy∈H)"

Dans y^-1gy mon esprit s'entête à considérer "g" comme un "objet" manipulé par des actions y. Si je lâche cette bride, ça devient plus simple.

Je te rappelle qu'au niveau [⚤] un ("objet" est synchronique)_⚤, quand une ("action" est diachronique)_⇅.

Or ce matin, j'ai pris conscience qu'en fait,

1. Nous réifions en [⚤] l'action diachronique [∃]⇅[⚤]_⇅𓁜;
2. En 𓁝_⇅[#] nous ne percevons plus les objets que par les actions que nous leur faisons subir !

- Mais ne sommes-nous pas ici en [⚤]?

- Oui, après une régression 𓁝_⇅[#]⏩𓁝_⇅[⚤] qu'il faut comprendre. J'ai dit qu'en 𓁝_⇅[⚤] nous ne pouvions plus voir les "éléments" d'un ensemble que comme éléments d'un groupe quotient, tels que Z/nZ, pour fixer les idées. Mais c'est une façon de réifier l'action du Sujet, qui consiste essentiellement à des allers-retours section/rétraction, comme nous l'avons vu.

• Dans la position [∃]⇅[⚤]_⇅𓁜 nous pouvons parler de l'action ⇅ sur un "objet" puisque nous postulons son existence en [∃],
• Dans la position 𓁝_⇅[⚤](...)[∅], cet objet fait défaut, et donc nous ne pouvons plus traiter que de l'action elle-même.

- Et ton objet Z/nZ ?

- Il faut le considérer comme regroupant et réifiant les actions qui en assurent la cohérence. De même qu'en [♲]​​​​​​ les éléments de géométries sont la réification d'actions stables (qui ramènent à la même place). Point de vue qui recoupe d'ailleurs celui de Poincaré, lorsqu'il introduit la géométrie par les "actions".

D'une certaine façon, lorsque l'on s'éloigne de la logique élémentaire, au niveau de la Catégorie des Ensembles, faute de pouvoir nous référer à l'objet final (*)_∃, le Sujet est condamné à ne parler que de lui-même !

- Voilà qui est radical !

- Pense à ceci : l'homme a développé son cerveau animal pour organiser son action. C'est à l'origine un chasseur-cueilleur qui économise ses efforts pour survivre. Note bien que ce n'est pas propre à l'Homme et ne date pas de l'acquisition du langage, comme le prouve notre expérience sur des chats.

- Nous manipulons pourtant des concepts "objectifs" comme des droites, des points etc.

- Oui, par souci d'efficacité. C'est d'ailleurs l'objectif du niveau [♲]​​​​​​ où nous reconstruisons des "quantités" tels que le "poids" d'une pomme, le "prix" d'un aspirateur, un "volume" de mayonnaise, la "surface" d'un pré... Mais nous intéressant ici au Sujet lui-même, il convient de gratter cet habillage pour comprendre comment tout ceci est agencé; et je te dis que faute d'élément, un "objet" dont le référé ultime ( )_∅ est vide, ne peut être qu'une réification des mouvements qui le cernent ou le connotent.

- J'ai le sentiment que tu vis ces jours-ci une évolution radicale de ta pensée, et lorsque nous en reviendrons à la physique, ce ne sera plus un soupçon de relativité par rapport au Sujet qu'il faudra ajouter à la physique de l'objet, mais toute la physique qu'il conviendra de raccrocher à la psychologie du Sujet...

- Il n'y a pas de "juste milieu" entre Bohr et Einstein, et quant à suivre Bohr, comme nous le faisons, alors autant aller au bout de son raisonnement. 

Quittons pour un instant le langage mathématique pour parler de nos trois niveaux Imaginaires centraux : [⚤][#][♲]​​​​​​.

• La première étape [⚤], consiste à porter des jugements simples, dichotomiques sur nos stimuli.
• La seconde [#] consiste à admettre que certaines choses apparemment contradictoires peuvent coexister, quoique étrangères entre elles. Une femme peut être potière et jalouse, comme la mayonnaise contenir de l'huile et de l'eau.
• La troisième [♲]​​​​​​ consiste à concilier ce qui est étranger pour le manipuler aisément. Le prix des choses permet d'échanger un Rembrandt comme quelques tonnes de citrons.

Et bien, ma thèse consistera à vérifier que cet étagement facilite la compréhension de la physique, et que l'on retrouve l'articulation entre ces trois niveaux dans le langage mathématique.

- Et l'étape qui te pose du souci est celle du passage de [#] à [⚤], merci j'ai compris. Bref, tu radicalises le changement de paradigme, mais tu n'as pas avancé d'un iota aujourd'hui...

​​​​Le 23/12/2020 :

- En m'éveillant ce matin, il m'a semblé que la représentation sur laquelle je m'acharne depuis un moment est erronée, et qu'il faut repartir avec Étienne Ghys de cette vidéo sur les revêtements, qui nous a déjà passablement servi (note 10):

- Peux-tu préciser le point d'achoppement ?

- Dans les représentations de H et G, auxquels fait référence notre définition des groupes distingués :

"soit G un groupe, et H un sous groupe de G, ce dernier est distingué si (∀y∈G I y^-1Hy∈H)",

j'hésite sur la place relative de G et H. J'ai bien conscience qu'il doivent être représentés "orthogonalement" l'un à l'autre, avec l'élément neutre comme point de contact commun, mais, sur le schéma au tableau de Ghys, lequel est horizontal (une soucoupe U_i), lequel est vertical (reprenant les actions de section/ rétraction, ou projection et projection^-1) ?

• L'écriture yy^-1 me porte à "voir" G comme vertical ( avec un va-et-vient entre y et y^-1 vertical (comme les projections π et π^-1), et H horizontal, en gros comme une "coupe" U_i de H;
• Mais l'idée que "tous les éléments de G" sont idempotents, vus de la base B, me conduit à les voir comme étagés verticalement, pour se projeter en un seul et unique point de B, et G serait dans ce cas un ensemble "vertical".

- Si tu réussis à exprimer ce sur quoi tu butes, tu ne devrais pas être loin de résoudre ton problème... Essaie en 4D...

- Comment cela ?

- Je n'en sais rien, c'est toi l'auteur, mais lorsqu'une figure semble impossible, comme de représenter un noeud en 2D, la plonger dans un espace plus grand permet d'élargir l'horizon, si je puis dire.

- Autrement dit, nous pourrions avoir plusieurs coupes orthogonales en 3D d'un référé en 4D?

- Essayons. 

Le 24/12/2020 :

- J'ai passé la journée d'hier avec cette idée qui roulait dans ma tête comme un caillou sous la langue d'Ésope, pour me rendre compte une fois de plus combien mon esprit est limité par une vie asservie à la simple logique.

- Mais encore ?

- Mes yeux me montrent une forme ygy^-1 ressemblant à s'y méprendre à πyπ^-1 par laquelle on rattache un espace topologique X à sa base B, et bien soit : convenons que l'action y sur g rabatte les éléments de H sur G de la même façon que les projections π rabattent X sur B, et voilà tout.

- Mais il n'y a qu'une base B alors que l'ensemble H peut être constitué de plusieurs sous-groupes G...

- C'est dire tout simplement que notre vision de H à partir de G est locale: 𓁝_⇅[⚤].

- Et qu'en est-il de la position adoptée pour rabattre un espace topologique X sur sa base B ?

- Le point de départ est local, mais dans une pensée purement topologique 𓁝_⇅[#], que l'on exprime algébriquement après un retournement du Sujet : [⚤]𓁝_⇅𓁜[#]⏩[⚤]𓁝_⇅𓁜[#], et donc la position d'arrivée est globale !

J'ai en fait deux discours topologiques 𓁝_⇅[#] et 𓁝_⇅[⚤] portant sur le même objet H, se traduisant chacun par une écriture algébrique [⚤]_⇅𓁜 -Point barre-

- Tu veux dire que tu m'as traîné tout un mois au fil de cet article pour en arriver à cette banalité ?

- Bah oui. Si tu le relis à présent, tu vas te dire à chaque ligne "quel imbécile, il ne voit donc pas ce qui crève les yeux ?". 

Mais je vais te dire: si je n'étais pas cet imbécile borné, je ne chercherais pas à comprendre ce qui m'échappe, et mon "intuition" des choses ne me permettrait pas, comme ici, de mettre à plat mes postures dans mon discours, pour nettoyer la bande son de toute dissonance, diaphonie ou Larsen.

C'est un peu comme un autiste qui doit régler le tuning et s'accorder aux autres pour comprendre_⚤ ce que les gens "normaux" ressentent_♲ sans effort.

- En somme, tu es un autiste des maths ?

- On peut le voir comme ça.

- Bien, maintenant que nous avons défini les différentes postures du discours, nous pourrons peut-être aller un peu plus vite !

- Nous sommes donc dans cette position locale 𓁝_⇅[⚤] pour "distinguer" un sous-groupe dans un groupe. Maintenant, comme je ne cesse de le rabâcher dans cet article, il s'agit d'une position dégénérée, qui singe la position 𓁝_⇅[#], mais l'algèbre proprement dite s'exprime quant à elle ex post [⚤]_⇅𓁜, et c'est de cela dont nous parle Jesua Epequin, dans cette vidéo que je ne cesse de repousser en fin d'article, dans l'attente d'y revenir :

- Là, il n'y a pas de doute : il nous parle d'algèbre !

- Oui, certes, mais tu remarqueras qu'il ne nous dit rien du pourquoi des choses.

Quelle est la signification profonde du concept de sous-groupe distingué ? 

Quelle est l'utilité de définir des classes construites dans G à partir de H⊂G telles que :

• Classes à droites : x ∈ G : xH=  {xh|h∈H}
• Classes à gauche : x ∈ G : Hx=  {hx|h∈H}

Comprends-tu ma frustration ? J'entends un virtuose qui ne me transmet aucune émotion, rien, le langage (même mathématique) reste du volapük, tant qu'il n'exprime pas d'intention.

- À quoi t'attendais-tu ?

- À comprendre en quoi cela nous parle de symétrie bien sûr; reviens à notre petit schéma :

Nous devons reprendre quelque peu cette a priori :

• (2) doit s'écrire : (𓁝_⇅[♲]_⇆𓁜⏩𓁝_⇅𓁜[♲]_⇆𓁜⏩[⚤]𓁝_⇅𓁜⏩𓁝_⇅[⚤]_⇅𓁜)𓂀, l'aboutissement étant en  𓁝_⇅[⚤] et non [⚤]_⇅𓁜. La notion de symétrie_♲, d'ordre visuel, tirée de la géométrie_#, plus qu'opposition dialectique_⚤, devait nécessairement respecter cette approche duale 𓁝_⇅𓁜, propre à une approche topologique_#, eût-elle régressé au niveau [⚤].
• (3) décrit le mouvement que fait le Sujet pour exprimer algébriquement_⚤ la vision topologique_# d'un espace topologique X, vu comme une collection de revêtements U_i.

Tout ceci nous conforte dans l'idée que [♲]_⇆𓁜 est la position adoptée par le Sujet pour établir une équivalence entre deux expressions de la symétrie :

• 𓁝_⇅[#]_⊥𓁜⏩[#]𓁝_⊥𓁜[♲]_⇆𓁜⏩𓁝_⊥[♲]_⇆𓁜⏩𓁝_⊥[♲]_⇆𓁜 tiré de l'expérience individuelle du miroir 𓁝_⊥𓁜 par chaque individu ;
• 𓁝_⇅[⚤]_⇅𓁜⏩...⏩[♲]⇆𓁜, qui n'est autre que l'expression précédente inversée (2)^-1, reflétant le point de vue d'un maître, celui d'Évariste Galois établissant sa théorie des groupes de symétries.

- Mais finalement, en quoi consiste le concept de symétrie ?

- J'ai le sentiment que c'est le déclic ressenti par l'enfant, lorsque se voyant dans le miroir [#]𓁝_⊥𓁜 il comprend d'un coup qu'il est pour l'Autre comme son reflet pour lui 𓁝_⊥[♲]⏩[♲]⇆𓁜. La prise de conscience par laquelle il se constitue comme Sujet étant la quantité invariante_♲ liée à ce retournement sur lui-même  (𓁝_⊥I⇆𓁜)_♲ pour se voir dans le regard de l'Autre .

- Tu utilises le vocabulaire de Noether?

- Nécessairement, puisque je suis moi-même en [♲]_⇆𓂀 pour l'écrire.

Autrement dit :

l'essence de la symétrie_♲ est  la conservation du mouvement_♲ du Sujet ex ante/ ex post autour du niveau synchronique [♲].

- Conservation du Sujet ou de l'objet ?

- Les deux mon capitaine, nous en avons déjà discuté ci-dessus.

- D'accord, mais alors, parle-nous de la symétrie concernant les objets.

- Nous repérons un objet par les symétries_♲ que nous y voyons et nous permettent de le mémoriser;  dit autrement, l'existence_♲ que nous attribuons à un objet résulte de sa stabilité, c.-à-d. de sa permanence à travers nos mouvements autour de lui ou les transformations que nous lui faisons subir.

- Il s'agit donc toujours, in fine, d'une question d'existence de l'objet pour le Sujet?

- Oui, toujours.

- Alors montre-nous la genèse du concept d'existence de l'objet à chaque niveau synchronique.

- Nous en avons déjà une bonne idée :

• En ☯[∃]𓁜, c'est l'axiome d'existence_∃=∃(*) du matheux, le "ergo sum" de Descartes  mais aussi la propriété universelle de la théorie des catégories;
• En 𓁝[∅]☯, avec l'idée d'existence_∅=∃( ) du vide exprimable ex ante 𓁝, nous quittons la pensée rationnelle pour aborder des questions liées à nos valeurs ou convictions d'ordre Symbolique ;
• En [♲]⇆𓁜 :
  • nous avons le triptyque de Noether : (symétrie/ quantité conservée/ indétermination)_♲ ; et existence_♲=quantité conservée_♲ ;
• En 𓁝_⇅[#]_⊥𓁜 :
  • En position _⊥𓁜 l'objet se détache de son environnement et existence_#=espace topologie_# comme collection des parties_# d'un objet-produit_# défini à partir de concepts orthogonaux ;
  • En position 𓁝_⇅, l'existence_⚤=stabilité_⚤ d'une partie_# d'un espace topologique_# se discute en termes de va-et-vient 𓁝_⇅|_⊥𓁜 identification/ idempotence ;
• En 𓁝_⇅[⚤]_⇅𓁜 enfin,
  • Dire en _⇅𓁜 qu'une partie d'un objet_# se conserve sous forme d'ensemble d'éléments_⚤ ou existence_⚤=objets-quotients_⚤
  • revient à constater 𓁝_⇅ que le sous-groupe des permutations_⚤ des éléments_⚤ qui y est attaché est distingué... existence_⚤=clôture_⚤ de G au sein de H;
  • Le renversement de perspective (𓁝_⇅𓁜)_⚤ s'exprime particulièrement bien sous forme matricielle (note 12), comme nous y invite la logique catégorique de Lawvere (note 13).

- Est-ce que par hasard cette approche duale 𓁝_⇅[⚤]_⇅𓁜 ne te rappelle pas la géométrie non-commutative d'Alain Connes ?

- Vas savoir...

Le 25/12/2020 :

- Cette dernière remarque, venant au fil de l'écriture, hier lorsque je cooconais tranquille et solitaire en ce réveillon de Noël m'a laissé sur le cul. Beau cadeau de Noël en vérité que cette pensée !

- Ton cerveau te la ressert juste à temps, parce que tu as tourné autour d'Alain Connes pendant quelque temps, tout simplement. (note 11)

- Je ne saurais te dire. Toujours est-il que j'ai calé en septembre sur sa présentation à des physiciens, faute de connaissances, et que je le retrouve ici pour des raisons extrêmement primaires de prise de conscience d'une symétrie_⚤ en position 𓁝_⇅.

Il y a cependant une question liée à cette régression de la géométrie de [#] à [⚤] qui est la disparition de l'hypothèse de la continuité_#.

- Tu avais déjà fait une remarque (voir note 9) sur son effacement en [♲].  Il semblerait alors que cette hypothèse soit strictement liée à l'apparition d'une posture locale  𓁝 en [#] et s'efface avec elle, en [⚤]𓁜 et [♲]𓁜.

- J'ai l'impression que nous y reviendrons très bientôt...

- Mais en attendant, pourrais-tu finaliser cet article cette année, en nous disant si  oui ou non, tu as fini par comprendre la nécessité de caractériser un sous-groupe distingué à partir de cette forme ygy^-1 ?

Le 02/01/2021 :

- Je n'ai pas réussi à tenir mon planning, et ce n'est que ce matin, en me rasant qu'une fois n'est pas coutume, tout c'est mis en place !

- À croire qu'inconsciemment tu voulais rester en échec ?

- Ne me distrais pas avec ce genre de pensées, sinon je vais perdre le fil.

Prends un groupe de symétrie tout simple, comme S3={e,(1,2), (1,3), (2,3), (123),(132)}, lorsque j'écris (2,3)^-1(1,2,3)(2,3)=(1,2,3), l'élément (1,2,3), doit être vu comme "objet" du discours, sur lequel s'exerce les "actions" (2,3) et (2,3)^-1, bien que tous ces éléments soient de même espèce, c'est-à-dire des permutations.

De ce point de vue, tu peux maintenant faire le rapprochement avec notre duo section/ rétraction, ou bien les projections π utilisées pour les faisceaux !

Il est là notre aplatissement du discours en [⚤], et la montée/ descente π/π^-1 ⇅ se retrouve dans une différence droite/ gauche liée à notre façon d'écrire.

De ce point de vue, un sous-groupe H est "distingué", lorsque l'action conjuguée d'un élément g de G sur l'un des éléments h de H, t'amène à un autre élément de H; et tu gardes bien cette idée d'idempotence entre éléments de H.

- C'est tout ? Un élève de lycée trouverait cela évident.

- Ben oui, je deviens sénile... Mes neurones tournent en béchamel et mes synapses sont aussi souples qu'un rail... De voir ma pensée filer sur des rails me désespère.

- Pourtant, il me semble bien qu'en écrivant cet article, tu étais proche de cette prise de conscience, lorsque tu parlais de l'objet en particulier.

- Effectivement. Cela tient à la définition de l'objet du discours. Nous en parlions déjà il y a deux semaines (voir x)

"- Il faudrait en déduire la nature de l'objet à partir de là :

• [∃][⚤]𓁜 : l'objet est une "collection d'éléments";
• [⚤][#]𓁜 : l'objet se définit comme "produit";
• [#][♲]𓁜 : l'objet se définit par sa "conservation";
• 𓁝[⚤][#] : l'objet se définit comme "groupe quotient";
• 𓁝[#][♲] : l'objet se définit par ses "parties";

- Fais de beaux rêves là-dessus..."

Dans notre appréhension la plus proche du Réel, nous considérons l'objet à la mode de Descartes, comme une horloge faite d'un assemblage de pignons et de roues. mais dès que l'on prend du recul pour nous interroger sur l'organisation même de cette mécanique, nous ne parlons plus de cet "objet" tiré du "Réel", mais de ses régularités, ou symétries, autrement dit, nous parlons plus de nous que de lui !

Les mots produit_#, conservation_♲, quotient_⚤, partie_# qualifient plus notre rapport à l'objet que ce dernier, et pour être encore plus précis, il conviendrait de noter non seulement en indice le niveau synchronique auquel ils se rattachent mais également en exposant, la posture du Sujet à leur égard.

Pour alléger l'écriture, prenons la convention suivante : 

• Un concept_α noté sans exposant est implicitement vu ex post [α]𓁜;
• Un concept vu ex ante en 𓁝[α] par sera noté ^𓁝concept_α.  

Ce qui nous donne :

• [∃][⚤]𓁜 : l'objet_⚤ est un ensemble_⚤ d'éléments_⚤ ;
• [⚤][#]𓁜 : l'objet_# se définit comme produit_# (cartésien);
• [#][♲]​​​​​​𓁜 : l'objet_♲ se définit par sa conservation_♲ (Noether);
• 𓁝[⚤][#] : l'^𓁝objet_⚤ se définit comme ^𓁝groupe quotient_⚤ ;
• 𓁝[#][♲]​​​​​​ : l'^𓁝objet_# se définit par ses ^𓁝parties_# ;

Cette façon de définir précisément à quel niveau synchronique se situe l'objet du discours et dans quel posture du Sujet il est envisagé, permettrait sans doute d'éviter bien des confusions.

- En l'occurrence, à quoi cette notation très détaillée pourrait-elle nous servir?

- Nous sommes ici en train de parler du gap entre niveaux [⚤] et [#], mais pour respecter nos principes très généraux de symétrie, de niveau [♲]​​​​​​, je pense qu'il faudrait mettre en perspective les deux situations [∃][⚤]𓁜 et 𓁝[⚤][#] afin de comprendre leur différence en termes de brisure de symétrie.

- Tu radotes, nous en avons déjà parlé le 07/12 (voir y) :

La régression de [#] à  [⚤] peut être vue en [♲]​​​​​​𓂀 comme une rupture de symétrie entre les séquences ↑↓ et ↓↑ au niveau [⚤]. 

- Oui, oui, je veux juste repérer cette différence dans la façon de définir groupe et sous-groupe distingué. En écrivant que H est un sous-groupe distingué de G (ou H⊴G) :

• Le groupe G est décrit en identifiant directement ses éléments, dans la position  [∃][⚤]𓁜, et on peut écrire "le groupe G_⚤"
• Le sous-groupe H est défini :
  • par l'idempotence de ses éléments, (et non plus par leur identification)
  • avec une équivalence entre les séquences  ↑↓ et ↓↑, ramenée ici à l'équivalence entre partitions droite et gauche de G.
  • Autrement dit, le sous-groupe est défini dans la position 𓁝[⚤][#], et l'on doit écrire "le sous-groupe distingué ^𓁝H_⚤"

Il y a donc entre l'objet ^𓁝H_⚤ et l'objet G_⚤, une rupture de symétrie dans la façon de les appréhender, qui d'un point de vue très général [♲]​​​​​​𓂀 doit s'exprimer grâce au triptyque de Noether :

• La symétrie est celle entre   ↑↓ et ↓↑ ​​​​​​;
• La quantité conservée est le sous-groupe H ;
• L'incertitude est ici l'idempotence entre les éléments du sous-groupe H.

- Bon, cette fois-ci, je crois qu'il est temps de passer à autre chose !

- Oui, je pense avoir mieux cerné le concept de symétrie et ses déclinaisons en régressant de [♲]​​​​​​𓁜 à [⚤]𓁜.

Bonne rumination à tous et bonne année !

Hari

Note 1 :

Voir :

• "Identité et idempotence"

Note 2 :

Mes développements se resserrent autour des questions d'homologie :

• "Les groupes d'homologie du Sujet #3" 01/09/2020
• "Les groupes d'homologie du Sujet #2" 01/04/2020
• "Les groupes d'homologie du Sujet"  14/11/2019

Note 3 :

Voir

• "Aspects de la géométrie"

Note 4 :

Cédric Villani introduit son cours sur la courbure de Ricci par une réflexion sur ce problème :

• "La narration en relativité"

Note 5 :

En écrivant ceci, je me demande si l'on ne pourrait pas distinguer l'indétermination liée à [∃]⇅[⚤]𓁜 de celle liée à [⚤]⇅[#]𓁜 ou à [#]⇅ [♲]​​​​​​𓁜.

• [∃]⇅[⚤]𓁜 conduit directement au principe d'incertitude concernant le repérage de l'espace et du temps (voir "Le principe d'incertitude sans les maths";
• [⚤]⇅[#]𓁜 introduit la notion de rotation, repérable en C où la répétition du même est une rotation, avec le choix pour arriver à l'identité 1 entre e^2iπ et e^-2iπ ; d'où la tentation d'y associer la notion de spin...

- Quid de la répétition du dernier mouvement [#]⇅[♲]​​​​​​𓁜?

- Laisse-moi le temps d'y réfléchir... A priori, je dirais que l'Imaginaire se déplie en [⚤] et [#] quant il se ressert en [♲]​​​​​​. En ce sens, la répétition n'y jouerait plus le même rôle. Il ne s'agirait plus d'explorer les possibles, mais au contraire de resserrer l'Imaginaire autour de principes d'autant plus solides qu'ils se retrouvent partout, pour préparer le saut final vers [∅], voir ☯ pour les plus ambitieux...

Relecture au 30/12 :

Et si l'indétermination propre au niveau [♲]​​​​​​ tenait tout simplement à l'abandon de l'hypothèse de la continuité qui s'était imposée dans la posture  𓁝[#]? 

Ce qui nous ramènerait aux considérations de la note 9 ci-dessous !

Dans cette perspective, l'apparition de l'hypothèse du continu en [#] dans un saut récessif [♲]​​​​​​↓[#] marquerait une rupture de symétrie entre continu/ discontinu.

- Il resterait à définir la quantité conservée attachée à cette symétrie !

- L'idée qui me vient à chaud est celle-ci :

le vide n'est ni continu, ni discontinu...

Cela me semble une bonne base pour définir un retournement initial [♲]​​​​​​𓁝𓁜[∅]⏩[♲]​​​​​​𓁝𓁜[∅], et dans cette perspective, le vide serait la quantité conservée, on ne peut rêver plus bel oxymore, qu'en penses-tu?

- Peut-on parler du vide en termes de "quantité conservée" ?

- Oui et non, d'où sans doute les "fluctuations quantiques" et la possibilité d'un Big Bang issu du néant... 

- Il y a là un sujet à creuser : de quelle façon s'évanouissent les axiomes que nous bricolons pour étayer notre imaginaire lorsque l'on s'approche de l'objet initial vide ?

- Tu as raison, et ceci nous ramène directement à la pensée de Lao Tseu. (voir "Tao Te King et Dharma" daté du 20/02/2008 ce qui ne me rajeunit pas!).

Je retiens l'idée d'une exploration des axiomes que nous utilisons dans cette perspective : existence, choix, continuité, infini, double négation etc...

D'une façon générale, "tout doit disparaître" en abordant 𓁝[∅] comme un commerçant fait place nette lors des soldes pour accueillir sa nouvelle collection.

- Dans ce cas, même le triptyque de Noether doit disparaître ...

- C'est sans doute le dernier principe à s'effacer avant de laisser libre la scène finale pour le spectacle suivant. 

• La conservation_∅ du vide est en soi, comme nos l'avons déjà vu un oxymore, autrement dit un non-sens;
• Par ailleurs, la notion de symétrie_∅ n'a plus de sens en 𓁝[∅], faute d'axe ou de point permettant de contempler l'image du vide;
• L'indétermination_∅ n'a plus de sens non plus, faute de Sujet en position ex post [∅]𓁜 pour en parler rationnellement.

Plus tard dans la journée...

Encoussiné dans mon canapé, alors que je fais une sieste tranquille sous les rayons du soleil d'hiver, le chat gratte délicatement à la vitre de la porte-fenêtre pour rentrer. Il a du gratter depuis un petit moment pour que le bruit soyeux des pattes sur le double vitrage s'infiltre dans mes neurones... Après lui avoir ouvert, je jette un oeil sur Facebook, pour me réveiller en douceur et tombe sur cette vidéo d'un Yogi :

J'ai beau "savoir" qu'il n'y a pas de hasard, là j'en suis quand même surpris ! Sais-tu la signification du mot "Bouddha"?

"Bou" veut dire "buddhi"
"da" veut dire "dhadha"
"buddhi" veut dire "intellect"
"dhadha" veut dire "quelqu'un qui est au-dessus"
Quelqu'un qui est dans son intellect est un être humain continuellement souffrant(...)
Si vous êtes en dessous du mental, on vous appelle "buddhu", vous passez à côté.

Vois-tu la très grande proximité avec notre approche ?

Nous pourrions imaginer que notre petit scribe 𓁝 ou "buddhu" en-dessous de son intellect, devienne "bouddha" 𓁜 passant en position "dhadha"... Ceci cadre parfaitement avec cette sortie de la pensée rationnelle que constituerait le saut 𓁝[∅]⏩[∅]𓁜, ou prise de conscience par le Sujet da sa propre vacuité...

- Ce "dhadha", me rappelle le "da" du jeu de "fort/da" du petit Ernst, rapporté par Freud, avec la même opposition vocale entre un son fermé (o/ou) et un ouvert (a)...

- Oui, aussi, mais là tu reviens bien en arrière ! 

Note 6 :

Voir :

• "Le point #8 - Logique - topologie"

Note 7 :

J'ai pas mal écrit sur la structure de l'Imaginaire, voir en particulier r:

• "L'Imaginaire fractal" du 07/02/2015

Note 8 :

Voir : 

•  "Présentation du 12 juin au groupe de travail "Logique catégorique" du 06/06/2019

Note 9 :

- Pendant que nous en sommes d'évoquer la mécanique quantique, je repense à une marotte de NJ Wildberger : son refus du continu pour en rester aux nombres rationnels.

Je pense que l'on ne peut pas éviter l'hypothèse de la continuité en [#], tout simplement à cause de la position ex ante du Sujet, tourné vers l'objet initial 𓁝[#][∅].

Ceci dit, la question reste ouverte en [∃][♲]​​​​​​𓁜.

- Attends, une fois un concept acquis, tu ne peux plus l'oublier !

- Eh bien cela se discute à mon sens... Repense à la perte de la notion d'ordre lorsque tu passes de R à C par exemple...

- Pourquoi cette note ?

- Parce qu'en parlant de rotation dans le plan complexe, et surtout de symétrie par rapport à une droite, je me suis souvenu de cet argument de NJ Wildberger :

Je te la fais courte :

Si les éléments de la géométrie sont construits à partir de symétries, par rapport à un axe, alors, on définit les points sur le cercle unité par des angles doubles de la pente θ de cet axe. Soit z=e^iθ son point d'intersection sur le cercle unité, alors le point défini par l'axiomatique de Bachmann est en z=e^i2θ !

Or, NJ Wildberger montre assez facilement que dans ce cas, il n'est pas besoin de la continuité en R, et que l'on peut se limiter à l'usage des nombres rationnels Q pour faire de la géométrie...

- Attends un peu, oui pour les "objets" tels que points et droites, mais pas pour ton axe de symétrie...

- Je me demande s'il n'est pas là le lit commun du discret et du continu ?

Vois-tu le champ de réflexions qui s'ouvre à nous ?

Après la perte de la l'orde en [#] quand apparaît la nécessité de la continuité, voici que cette hypothèse ne serait plus de mise en [♲]​​​​​​... Et si la progression Imaginaire allait vers la simplification des concepts et non vers la complexité ?

Voilà qui irait fort bien avec l'idée d'une progression vers le l'objet initial, vide en [∅]...

- La philosophie n'est jamais loin des maths...

- J'allais le dire ! 

Note 10 :

Voir :

• "Identité et idempotence"

À propos d'Étienne Ghys, y repenser ce matin m'a donné envie de visionné quelques vidéo de ses conférences, qui m'ont enthousiasmé, au point que je lui ai adressé un mail pour attirer son attention sur ma démarche. L'avenir nous dira si cette bouteille à la mer a été utile ou pas...

Note 11 :

Voir :

• "Rencontrer Alain Connes" du 07/09/2020
• "Comment aborder la géométrie non-commutative #1" du 08/09/2020
• "Géométrie non-commutative #2" du 09/09/2020
• "Géométrie non-commutative #3" du 08/08 au 06/10/2020

Exploration qui s'était soldée par un constat d'échec, faute d'une bonne connaissance de la théorie de la mesure.

Note 12 :

Voir :

• "Matrice"

Note 13 :

En écrivant cela, je me rends compte qu'il me faut préciser la posture du Sujet exprimant l'objet discriminant élémentaire {(*),( )}_⚤.

1. L'identification de l'objet final (*)_∃↑{*}_⚤ est effectivement une action très primaire du Sujet, en position [∃][⚤]⇅𓁜;
2. Mais l'idée des "parties" de l'objet final, qui introduit son complément vide {( )}, ne vient qu'après le stade du miroir, comme résultant d'une dégénérescence de la position topologique locale :
   • [⚤]𓁝⇅​​​​​​​𓁜 [#]⏩[⚤]𓁝⇅​​​​​​​𓁜 [#]⏩𓁝⇅​​​​​​[⚤]⇅𓁜.

Processus intellectuel très marqué culturellement par lequel nous retrouvons, dans une pensée strictement rationnelle, (i.e.: bornée par 𓁜), une posture ex ante que nous connaissions depuis que l'Homme s'interroge 𓁝☯, et philosophe  𓁝|𓁜[∅]☯.

Nous constatons ainsi que la théorie des Catégories, même limitée à la rationalité logique de Lawvere, n'a pu se concevoir et s'exprimer historiquement, qu'après avec intériorisé la notion de parties_# d'un tout, d'un point de vue local topologique 𓁝⇅​​​​​​​[#]...

Cette mise en perspective inscrit alors l'objet discriminent dans une géométrie non-commutative telle que je la comprends (i.e.: dans sa structure duale) .

La structure générale de l'objet _𓁝partie|élément_𓁜, que l'on a ici dans le topos de Lawvere au niveau [⚤], nous le retrouverons aussi sous la forme (Catégorie|revêtements) dans le topos de Grothendieck, à un niveau [#] ou [♲]​​​​​​ qui reste à préciser.

- À rapprocher de l'observable_⚤ du physicien, n'est-ce pas (voir "Les représentations du Sujet"), avec cette écriture ⟨ | ⟩ qui rappelle un peu 𓁝|𓁜...

- Sans aucun doute. Nous en avions déjà un peu parler, et nous y reviendrons après avoir mieux compris Alain Connes, mais tu vois déjà qu'observable_⚤ et géométrie non-commutative_⚤ sous a priori de même niveau Imaginaire [⚤]...

Note 14 :

- Je ne pouvais pas en rester là, bien entendu. Après avoir revisité les axiomes de Bachmann le 20/12 et dormi quelque temps dessus, nous avons le temps d'y revenir à loisir en attendant le réveillon !

- Il me semblait que nous ne pouvions traiter que des produits de symétries de type 𓁝|𓁜x𓁝[α]𓁜 (saut) ou 𓁝[α]𓁜x𓁝|𓁜 (régression) ?

- Oui, en restant moi-même 𓂀 dans une posture rationnelle logique [⚤]𓂀 avec l'idée d'une hiérarchie entre niveaux synchroniques [⚤][#][♲]​​​​​​; d'ailleurs l'antisymétrique des produits 𓁝|𓁜x𓁝[α]𓁜 et 𓁝[α]𓁜x𓁝|𓁜 l'indique assez.

Mais si nous essayons de mettre sur un "même plan" nos deux niveaux [⚤] et [#], de la même façon que Bachmann traite points et droites?

- Dans quelle posture serais-tu alors ?

- Puisqu'il s'agirait de mettre sur un même plan le discret en [⚤] et le continu en [#], correspondant à la dualité point/ droite en géométrie, je pense que je serais dans une posture [♲]​​​​​​𓂀.

- Soit, essayons donc...

Quel serait le produit de deux rotations de type 𓁝|𓁜 ?

- S'il s'agit :

1. du même point de pivotement, soit ⇅, ⊥ ou  ⇆, tu reviens à ta position initiale (ou l'identité_♲) : 𓁝|𓁜x𓁝|𓁜=e ; d'ordre 2 ou stable par conjugaison;
2. de deux points de pivotements différents :  𓁝⇅𓁜x𓁝⊥𓁜 ou 𓁝⇅𓁜x𓁝⇆𓁜 ou 𓁝⊥𓁜x𓁝⇆𓁜 il y a une rupture inconsciente pour passer d'un concept diachronique à l'autre, et le produit n'est pas rationnel. Tu retrouves l'idée que le produit de deux symétries radiales autour de points différents n'est jamais d'ordre 2.

De ce point de vue, le Sujet serait le produit redoublé d'un mouvement : Sujet_♲=(𓁝|𓁜)², tu retrouves l'idée de la constitution du Sujet par un retour sur lui-même dans l'expérience du miroir. 

- Quid du produit 𓁝[α]𓁜x𓁝[β]𓁜 ?

- Là encore, il faut distinguer les cas β=α et β≠α.

1. β=α alors, (𓁝[α]𓁜)² ramène le Sujet à sa position initiale. Même constat que précédemment : (𓁝[α]​​​​​​​𓁜)²=e; d'ordre 2 ou stable par conjugaison.
2. β≠α.

C'est dans ce dernier cas que notre point de vue [♲]𓂀 s'écarterait de la rationalité logique, ou approche immanente classique : [⚤]𓂀.

- Je ne te suis plus ?

- Il faut que moi 𓂀, auteur de ce discours sur le Sujet, en position [♲]𓂀 je considère comme équivalentes_♲ou orthogonales_# entre elles (i.e.: indépendantes) les postures du Sujet [⚤]𓁜, [#]𓁜, [♲]𓁜; ce dont le sujet lui-même est incapable, puisque pour lui elles sont dépendantes ! C'est tout du moins ce à quoi l'axiomatique de Bachmann nous invite.

- D'accord, et ça te mène où ?

- Il faudrait dépasser le point où nous en étions restés; je reprends :

• (a) : (dichotomie_⚤⇅[#] ⇆orthogonalité_#)𓂀
• (b) : (orthogonalité_#⊥[♲]⇆conservation_♲)𓂀
• (c)=(a)(b) : (dichotomie_⚤[#][♲] ⇆conservation_♲)𓂀

- Qu'entends-tu par "dépasser" ?

- Nous n'avons envisagé qu'un seul produit ⇅[#]x⊥[♲] ; mais comment sauter directement de  [♲] à [⚤] vu dans une sorte de circularité, et non plus comme une régression ?

- Tu en reviens à ta bouteille de Klein ?

- Oui, certainement... J'avoue qu'il y a du travail pour y arriver !