Topologie Part 1 - morphisme / comorphisme

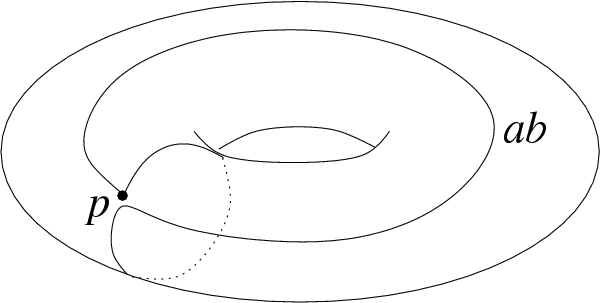
- Mais dis-moi,  si je te sens plutôt à l'aise dans ces espaces vectoriels que tu viens de présenter, je ne vois pas trop clairement le lien avec la géométrie.

- Oui, cela vient de ma formation d'ingénieur. Mais je me rends compte en écrivant que  la complexité des outils de l'ingénieur dépasse largement la connaissance qu'il en a ! C'est comme d'utiliser son iPhone sans la moindre idée de ce qu'est un semi-conducteur. Et j'avoue  qu'en contemplant notre tableau général des "structures" je m'effraie un peu en constatant que nous n'avons couvert que les premières branches de la partie droite.

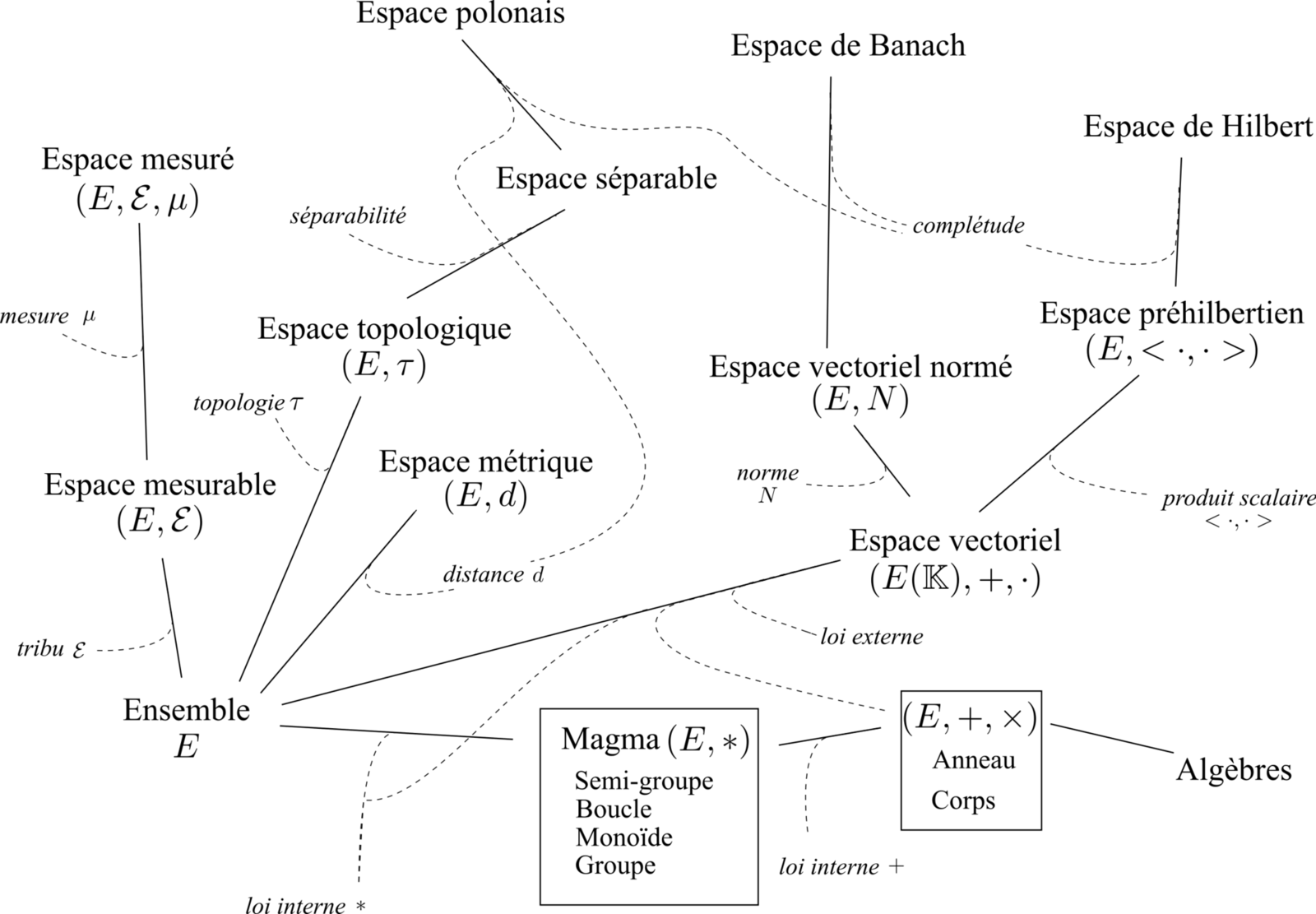
Nous nous sommes focalisés sur l'aspect algébrique des structures, qui se définissent à partir de I01, comme nous venons de le voir. L'idée de la topologie algébrique étant de construire les figures d'un espace affine à partir de mouvements décrits par des vecteurs (voir "du vecteur à l'espace affine").

Sur la gauche de notre taxinomie, les structures d'espaces sont directement rattachées aux Ensembles. Leur construction demande immédiatement d'énoncer l'hypothèse du continu, car l'outil primitif que l'on utilise pour repérer un point, c'est le concept d' "ouvert", et l'on procède par recouvrements de plus en plus serrés pour le coincer dans les mailles d'un filet. Or, les opérations sur ces recouvrements sont de type additif. Nous laissons tomber pour l'instant tout ce qui a trait aux questions de norme, mesure, métrique, surface, produit vectoriel, qui relève d'un niveau supérieur à IR, que nous avons déjà grossièrement repéré par I#, c'est-à-dire celui où l'on peut imaginer des structures simplectiques (voir "sur la simplectisation de la physique").

Il faut donc nous intéresser maintenant à ce que l'on nomme "espace topologique".

Mais nous pouvons déjà nous faire la réflexion suivante : 

Dans un espace vectoriel: 

• Le vecteur sert à décrire un saut diachronique portant de I01 à IR; 
• La multiplication s'enrichit : de simple répétition du même entre I1 et I01, elle devient multiplication extérieure entre I01 et IR;
• L'addition vectorielle garde la structure de l'addition scalaire.

Autrement dit, nous gardons un lien permettant de structurer les objets en IR, à partir de I01, avec cette remarque fondamentale que la structure est au moins d'un pas en retard sur l'objet qu'elle traite: un premier saut I01=>IR permet d'énoncer l'hypothèse du continu, un second saut permet de créer un espace vectoriel sur un corps K qui soit R (les réels) ou C (les complexes).

Dans un espace topologique :

Il n'y a aucune "passerelle" entre I01 et IR, car dès le premier saut, l'hypothèse du continu est énoncée par Im (i.e.: un choix IR<Im). Et donc :

• Les structures que nous pourrons y définir sont de pures métaphores de celles décrites en I01;
• L'objet auquel on va se référer n'est pas l'objet final, en I1, puisque nous coupons les ponts entre IR et I01, mais l'objet initial, en I0, avec IR< I0;
• L'outil primitif n'est plus de type multiplicatif (centré sur l'objet final) mais additif, cernant l'objet initial.

Le problème fondamental tourne autour du traitement de l'objet initial { }. Et je pense qu'en l'explicitant ici de la façon la plus claire possible, nous nous faciliterons grandement le travail de fouilles auquel nous nous attelons.

1/ Par la "voie algébrique", nous privilégions la multiplication comme outil de construction à partir de l'élément final {*}. Pour reprendre Spinoza, il s'agit d'une démarche immanente.

• Du successeur entre {I1 ; I01}, on passe à
• La multiplication en I01, puis à
• La multiplication d'un vecteur par un scalaire entre  {I01; IR} qui est
• définie en IR.

Et le passage de la loi  ⊗ sur K, à la loi "." sur E est assuré par l'axiome d'associativité mixte de cette dernière par rapport à la loi ⊗ de K : (λ⊗η).u = λ ⊗ (η.u).

De plus, l'image de l'objet initial { } que l'on manipule, est ici définie en I01 comme partie de l'objet final {*}, Autrement dit, en I01, nous réussissons ce tour de force de "manipuler" l'image, le référent de { }. La structure abélienne de (E;+) en IR, reprend donc cette approche développée au niveau I01.

2/ Par la voie topologique, nous sommes coupés de cette approche immanente. Notre référé { }, est d'entrée de jeu situé en I0, avec IR < I0 = Im.

Et je suis bien obligé d'expliciter la position du Sujet pour éclairer mon discours, car si je situais ce dernier en IR, notre Sujet serait en position ex ante, dans une approche mythique de l'espace où il se trouve ! Par essence nous sommes ici dans une approche transcendante, toujours en pensant à Spinoza et à son entendement de deuxième espèce.

C'est ici qu'il faut situer la discussion que nous avions initiée dans le mon dernier billet sur la distinction local/ global. Et c'est là sans doute que notre approche permet d'exprimer les choses clairement et simplement. 

La première remarque tient à la place de Im. : compte tenu du fait que nous nous référons explicitement ou implicitement à { } situé en I0, et que d'autre part, nous sommes déjà arrivés à la conclusion que la plus haute position de Im était I0, (cf.: "l'élégance du vide") avant de basculer en position ex ante par rapport à son système symbolique, c.-à-d. dans un discours non rationnel, nous pouvons dire que pour tout discours portant sur la topologie, Im reste en position I0. Nous exploitons ici pleinement la distinction que nous avons établie au fur et à mesure de notre exploration, entre pensée logique / topologique (voir: "la mécanique de l'Imaginaire").

Ceci implique que pour se situer dans un espace qu'il "comprend", (i.e. dont Im a une vue globale en IR), le Sujet dois se dédoubler en Im' < Im avec IR=Im'. Cette situation duale Im'<Im se retrouvera pour les espaces d'ordre supérieur, en I#. Et donc, Im reste immobile en I0, quand Im' change de point de vue, soit IR ou I#, voire en I01, pour porter un regard topologique sur des espaces dégénérés, sans l'hypothèse du continu.

La seconde remarque tient à la prééminence de l'addition sur la multiplication. Faute de l'intuition du successeur, diachronique, qui se développe entre {I1 ; I01}, nous cernons l'objet initial à l'aide de "cribles" et le concept d'union, à plat en IR , est de l'ordre de l'addition, synchronique.

Dernière remarque et avant même d'entrer dans la définition d'une topologie, "attendez-vous à savoir", comme disait Genevive Tabouis, qu'une telle structure ne peut qu'être une métaphore d'une structure  utilisant une loi de composition interne additive (i.e.: avec le vide pour élément neutre), telles que nous avons pu les exprimer en I01.

Je suis désolé si cette présentation est un peu rabâchée, ce dont je me rends compte à la relecture. Je suis conscient d'avoir à la reformuler plus légèrement, mais aujourd'hui, j'avoue que l'écriture me sert de béquille dans mon exploration d'un domaine encore vierge à mes yeux. Mais il est grand temps de nous lancer.

Pour éviter de dire des bêtises dans un domaine totalement inconnu, je prends un cours destiné à des élèves de licence : "Introduction à la topologie" de Francis Nie et Dragos Iftimie à l'Université de Rennes 1.

Manque de chance, ils commencent par les espaces normés que j'ai volontairement laissés de côté pour l'instant. Approche déjà très structurée, comme en conviennent les auteurs, qui présentent ensuite la définition suivante d'un espace topologique :

"On appelle espace topologique un couple (X,O) où X est un ensemble et O une famille de parties de X. appelés "ouverts" tels que :

1. Toute réunion d'ouverts est un ouvert;
2. Une intersection finie d'ouverts est un ouvert;
3. X et Ø sont des ouverts."   

Ce qui m'amène immédiatement aux réflexions suivantes :
a/ La définition de l' "espace topologique" est une métaphore en IR, d'un discours tenu en I01 sur l'objet final {*}:

• X est un "ensemble" en I01 <=> {*} est un ensemble en I1;
• O en IR est une "famille de parties" de X <=> { ;*} est l'ensemble des parties de {*}, l'objet classifiant, en I01.

Parallèle qui induit, nous le verrons ci-dessous, une certaine ambiguïté concernant le positionnement de  Ø, qu'il convient de lever par un axiome.

b/ Le dernier axiome introduit X et Ø  dans la famille des Ouverts, au niveau IR, d'une façon qui répond à la construction de l'ensemble classifiant en I01 à partir de l'objet final:

Tu vois que, si notre définition induisait implicitement notre  Ø, comme partie de l'objet final, donc limité à I01, il est ici explicitement imposé par Im , en IR, en référence à l'objet initial  en I0, puisque, comme nous l'avons vu Im = I0 !

c/ Le premier axiome définit, comme je m'y attendais, une loi interne additive : i.e.: la réunion d'Ouverts.

d/ Le second axiome imposant la finitude de l'intersection, doit être rapproché de l'axiome 9 de fondation des Ensembles. (voir "des ensembles et des groupes").

Et donc, bien que la table de vérité de l'inclusion soit identique à celle d'une loi multiplicative, celle-ci doit se comprendre comme la déconstruction progressive d'un Ouvert déjà là; de même que l'axiome 9 de fondation, ou de régularité ,dans la théorie des Ensemble, s'assure que l'on revient à son point de départ.

• Déconstruire un ensemble signifie revenir à l'objet final {*};
• Déconstruire une famille d'Ouverts, signifie retrouver un élément de l'ensemble E.

Conclusion fondamentale :

Pour définir X à partir de ses éléments, on procède par une action multiplicative, l'action es ascendante I1 => I01; et la construction potentiellement infinie; pour le cerner à partir de familles d'Ouverts, on le "passe au crible" et l'action est descendante et finie : I01 <= IR.

- Ton approche me semble bien longue pour en arriver là !

- Et pourtant cela serre de très près la théorie des Catégories et nous permettra sans grande difficulté d'aborder très rapidement les topos de Grothendieck, mais ce qui m'intéresse dans l'immédiat, c'est de caractériser précisément cette différence d'approche de X, soit par le haut, soit par le bas.

- Pourtant morphisme et comorphismes se comprennent sans qu'il soit besoin de faire appel à l'hypothèse de la continuité.

- Absolument, et la topologie de Grothendieck n'y fait aucune référence. Toutefois, pour imaginer cette démarche descendante, il faut nécessairement partir d'un niveau au-dessus de I01, or c'est la condition nécessaire et suffisante pour pouvoir énoncer l'hypothèse du continu, qui reste un choix. Maintenant, que tu la choisisses ou pas, toujours est-il que la structure Imaginaire est en place, permettant de concevoir X comme résultat d'un comorphisme, et à Jean Leray de concevoir les faisceaux. Mais j'anticipe !

- Nous n'avons pas beaucoup avancé quant à la compréhension des travaux d'Évariste Galois !

- Je creuse, mon ami, je creuse ! Et c'est long... 

La suite au prochain numéro.

Hari