Temps, limite et co-limite

En mode zombi, juste au réveil, tout en ruminant la partie du chapitre 4 traitant du temps, retravaillée hier avec "Les Experts Miami" en fond sonore et sur laquelle je venais de rêvasser, je plie un peu de linge qui trainait par là et, rabattant le dernier pli d'une serviette que je tiens de je ne sais où, m'apparaît Tintin s'écriant hourra !

Le geste ponctuait pile-poil un rapprochement en gestation entre la représentation du temps et les questions de limite et co-limite dans la théorie des Catégories... J'y ai vu un signe.

Voici donc l'état de mes réflexions sur le sujet (que vous pouvez retrouver sur le chapitre 4 mis à jour) :

__________________________________________________________________________________

L’une des conséquences majeures du renversement de perspective opéré par la théorie des Catégories est de modifier celle du temps. Ce qui était de l’ordre de la succession dans l’expérience physique commune, devient un choix entre états potentiels.

- Explique un peu, je décroche.

- Assez curieusement, les auteurs de « Conceptual Mathematics » introduisent leur ouvrage en revenant, eux aussi, aux travaux de Galilée sur le mouvement, qu’ils définissent par une application du temps vers l’espace comme ceci :

Alors que je me sentais une certaine proximité avec des auteurs qui, comme moi, remontaient à Galilée, voilà que d’entrée de jeu, leur premier exemple bouscule toute mon approche ! Il m’a fallu méditer longtemps sur les apports de cette théorie pour revenir m’occuper de ce caillou coincé dans ma chaussure dès le premier pas !

Le problème tient à ce que le domaine d’un morphisme est par nécessité un objet, donc synchronique, alors que le temps est fondamentalement un concept diachronique…

Revenons en détail à ce bloc-notes qui a servi à ma démonstration. Pour « voir » le point mobile bouger, il me suffit de feuilleter les pages (en I_k), chacune marquée d’un point, et le sentiment de « mouvement » vient de leur superposition sur le bloc-notes (en I_{k + 1}). Quoique déjà dans l’Imaginaire, je n’ai pas besoin du langage pour appréhender ce mouvement : un chien le verrait comme moi.

Maintenant comment en « parler » de façon rigoureuse, avec la possibilité de faire des mesures ? Pour être cohérents, tentons de décrire cette opération par un morphisme.

• Le domaine c’est le bloc-notes dont les éléments sont les {pages} utilisées ;

• Le codomaine c’est l’ensemble N des entiers naturels, ou bien, de façon plus primitive comme sur le schéma précédent, une série de marques ou d’indices qui ordonne nos pages telle que {« top départ », « juste après », « top arrivée »}. Nous appellerons cet ensemble Chrono pour chronométrage.

• L’application consisterait à repérer chaque feuille du Bloc-notes par son indice dans le Chrono :

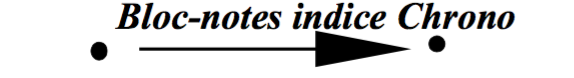
Le tour de passe-passe tient à la torsion opérée dans la relation de chaque objet à ses éléments :

• Pour le physicien le bloc-notes se reconstitue au fur et à mesure que les pages s’y accumulent. Le mouvement est séquentiel et le « temps physique », s’évalue par le nombre de fois où une page est rabattue sur le bloc-notes. Cette métaphore nous a conduits à définir le temps comme un concept purement diachronique.

• Pour le mathématicien qui, lui, s’occupe du chrono, l’indice d’une page est un élément de ce chrono donné d’avance.

L’instant présent qui s’inscrit pour le physicien dans une succession temporelle, devient pour le mathématicien l’actualisation d’une potentialité. Ce faisant, je restreins ma description d’un phénomène en devenir, virtuel par essence puisque le futur n’est jamais sûr, aux potentialités que je détermine par mon langage pour en rendre compte.

- C’est un peu tiré par les cheveux : lorsque tu dessines des points sur ton bloc-notes, celui-ci existe bel et bien, avant que tu ne l’utilises pour animer ta scène.

- Pas vraiment : on peut dire qu’il prend sens, pour moi et dans cette expérience, au fur et à mesure que les feuilles s’y empilent pour le constituer. L’objet physique vient à ma conscience, prend corps, par la répétition d’une action élémentaire.

- Rien de bien neuf : l’enfant prend conscience de la permanence de l’objet par la répétition¹, puis l’adulte vient à ses côtés pour plaquer un mot sur la chose.

- Exactement, c’est pour cela que mon discours t’a mis dans la confusion : lorsque tu m’objectes que le bloc-notes est déjà là, avant l’expérience, tu me retournes en fait le mot que j’ai employé pour te le désigner. Autrement dit, nous sommes déjà dans le discours. Mais pour le chien, qui voit comme moi le mouvement du point que je lui désigne, il s’agit seulement de quelque chose qui bouge par rapport à un environnement stable, de même qu’un taureau réagit aux mouvements de la muleta. Pour te rendre sensible à la chose, sans dire, dans un langage purement mathématique, que mon point se déplace dans un repère cartésien, le mot de bloc-notes m’est venu d’un coup à l’esprit comme métaphore de cet espace, où se déposerait un ensemble de feuilles d’épaisseur idéalement nulle. À partir de cette idée s’est développé le projet de me filmer faisant cette expérience dans un souci didactique, et si tu regardes la scène en question, tu verras qu’en fait de bloc-notes j’ai utilisé une pile de stickers jaunes par souci d’économie…

Tu vois bien comment se développe toute une dialectique entre cette idée de bloc-notes qui me vient d’un coup : le « ∃ bloc-notes » du matheux et la façon que j’ai de le reconstituer physiquement par un empilage de feuilles.

Toute représentation d’un mouvement suivra la même double démarche. Dans un film, par exemple, tu as d’un côté une « idée originale » que tu développes en « scénario », d’où tu tires un « synopsis » avec un découpage du récit en « scènes » puis en « plans », et de l’autre la réalisation qui commence par la recherche d’un « budget » et la constitution d’une « équipe », pour réaliser le « tournage » consistant à « mettre en scène » le « jeu » des acteurs, qui donnent des « rushs », aboutissant après « montage » à un ensemble ordonné d’images sur un support quelconque. L’objet « film », c’est la rencontre entre l’idée de départ et la projection séquentielle des images à l’arrivée.

- C’est un développement bien long qui nous éloigne de notre sujet, non ?

- Pas tant que cela puisque cette émergence progressive de l’objet physique à partir de la répétition rend vaine notre tentative de morphisme, car il me faudrait déclarer le domaine bloc-notes avant de construire mon morphisme et, de plus, que je tienne son identité pour acquise, ce qui reviendrait à constater son invariance !

Pour surmonter notre difficulté initiale due au fait que le temps ne peut pas être le domaine d’un morphisme dans la mesure où c’est un concept diachronique (i.e. : entre deux niveaux I_k et I_{k + 1}), j’ai cherché un objet bloc-notes pour le représenter ex post (i.e. : en I_{k + 1}), mais ce dernier reste en devenir dans le cours de l’action (i.e. : à chaque saut élémentaire I_k = > I_{k + 1}, l’objet se modifie) et je ne peux donc affirmer son identité qu’après la fin du mouvement ; mais dès lors, je suis complètement rentré dans le domaine de l’Imaginaire, parlant rétrospectivement d’un mouvement révolu, mort.

- Donc, quelle que soit la façon de présenter le problème, ton essai de morphisme « domaine- physique » = > « codomaine- mathématique » reste bancal…

- Oui, tu retrouves ici, à la charnière Réel / Imaginaire une limite symétrique à celle que nous avions repérée à l’autre bout de la chaîne, entre Imaginaire / Symbolique.

• Dans le saut Imaginaire = > Symbolique : impossible de définir un objet-codomaine ;

• Dans le saut Réel = > Imaginaire : impossible de définir un objet-domaine

C’est pourquoi je propose de remplacer le morphisme des auteurs (fig. 25), qui est de ce dernier type, par celui-ci, parfaitement constitué :

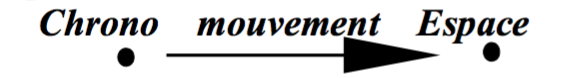
Maintenant, et c’est là où je voulais t’amener, passer d’un « temps » de l’ordre de la succession dans l’expérience physique commune, à un choix entre états potentiels dans notre Chrono marque une étape essentielle dans le développement de la physique.

Lorsque Galilée rapporte une fréquence de battement à son propre pouls, il fait un décompte. De là il peut parler de vitesse associée au principe d’inertie, comme nous l’avons vu. Newton ira plus loin et décrira les conditions de variations du mouvement. Nous sommes alors dans l’ordre de la succession, associé à une conception temporelle de la stabilité (i.e. : je lance en l’air une pièce et j’attends qu’elle retombe pour voir si j’ai tiré pile ou face).

Mais tu vois bien qu’en représentant le temps physique par un Chrono, je l’ai spatialisé : les états potentiels sont tous présents en même temps. Et le questionnement du physicien s’en trouve affecté ! C’est toute la démarche de Fermi en optique (le choix du plus court chemin), de Maupertuis en mécanique (le choix de moindre action), repris et développé ensuite par Lagrange et Hamilton, comme de Boltzmann en thermodynamique (l’état de plus faible énergie)¹…

C’est pourquoi je dis que la représentation de l’expérience physique par le langage mathématique lui est d’une certaine façon « orthogonale ». Le passage de l’expérience à sa représentation n’est pas uniquement de l’ordre d’une « montée diachronique d’un niveau synchronique à l’autre », mais nécessite la réification des concepts (ou référés) diachroniques en expressions (ou référents) synchroniques².

Eh bien, tout ceci est admirablement pris en compte, de la façon la plus élégante qui soit par la théorie des Catégories. Mieux : elle nous éclaire sur les voies de notre entendement.

- En bref, le concept de temps régresse, selon ton expression (i.e. : transformation synchronique = > diachronique) de l’Imaginaire vers le Réel, la limite étant le fait d’en parler, quand celui d’objet (transformation diachronique = > synchronique) vient à la conscience du Sujet à partir du Symbolique marqué par une déclaration d’existence.

- Oui, et c’est une grande question, liée au rapport entre l’objet et le temps !

- Tout ceci m’embrouille. Je me suis habitué à considérer l’espace et le temps comme des concepts duaux, propres à toute représentation du mouvement, et pour en revenir à Kant, comme des conditions de l’entendement, préexistantes à l’objet de discours et non pas liés à lui…

- Pourtant, ne viens-tu pas de me rappeler que chez l’enfant, l’objet se constitue à force de répétitions, donc au fil du temps ?

Reprends ce Bloc-notes qui nous a tant servis. Nous venons de voir qu’il se constitue selon deux modes très différents aux deux extrémités de notre Imaginaires.

• Du côté du perceptible mais non dicible, vers le Réel, il se constitue, feuille à feuille à partir d’un mouvement répétitif. Ce mouvement élémentaire, semblable à la tuchê lacanienne, liée comme il le dit à l’automaton, c’est-à-dire la répétition, nous l’avons réifié comme l’objet final  {.} ;

• Au plus près du Sujet, lorsqu’il en crée, ou se remémore, la représentation, en lui collant un nom : «Bloc-notes », nous avons vu qu’au-delà c’est le néant, l’objet initial { }.

Notre objet Bloc-notes se balade donc dans notre Imaginaire entre ces deux limites. Et bien, faute de pouvoir l’appréhender de façon charnelle, physique, à cause de l’absolue impossibilité de parler du temps sans le figer, nous tenterons de définir par quels chemins la description de cet objet particulier peut se ramener à cette base de référence que constituent les objets initial et final.

=> L’objet {.} en sera la limite et l’objet { } la colimite.

En fait, tout l’effort du mathématicien tend à apurer son discours de cet objet qui le gène parce qu’il lui échappe doublement : il se constitue avec le temps (avant le discours), pour ne prendre sens qu’aux yeux du Sujet (au-delà du discours). D’ailleurs, le projet de Saunders Mac Lane, dans son livre de référence¹, est bel et bien d’arriver à constituer une théorie des Catégories sans objets, à partir d’une « méta théorie des catégories ».

- Avec toutes ces considérations nous n’avons pas beaucoup avancé dans la théorie elle-même !

- Plus que tu ne crois ! Car nous verrons de quelle façon les limites de l’Imaginaire au contact du Réel et du Sujet, conditionnent les questionnements propres à la théorie ainsi que les objets qu’elle développe pour y répondre.

Par ailleurs, il importait de vérifier, dans ces premières définitions, s’il y avait un hiatus ou non entre cette théorie et notre démarche « entropologique ». Il semble au contraire avoir conforté l’a priori d’où nous sommes partis. Ceci étant fait, nous pouvons maintenant parler des règles de composition des morphismes.

___________________________________________________________________________________

Voilà ce fil rouge que je cherchais; ce qui structure le discours mathématique avec les mots de la théorie des Catégories: le lien entre objets initial et final, avec ces notions de limite / colimite qui mènent directement à la notion de multiplication...

Bon, tout ceci va encore mûrir, bien entendu, mais je pense être dans la bonne direction.

Au plaisir.

Hari.